 |
DIN-Papier und Goldener Schnitt
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
Welches sind die günstigsten Seitenverhältnisse für rechteckige Papierblätter
und Briefumschläge? Warum ist das Verhältnis der Seiten eines DIN-Papiers gleich Wurzel aus 2?
DIN-Formate (Rechtecke nach der DIN-Norm)
Günstig ist das Seitenverhältnis eines Blattes dann, wenn man es so in der Mitte durchschneiden
kann, dass die zwei entstehenden gleichen Blätter dem Ausgangsblatt ähnlich sind.
Wegen der geforderten Ähnlichkeit muss also das Verhältnis der längeren Seite a zu kürzeren Seite b des
Ausgangsblattes gleich dem Verhältnis der längeren Seite c zur kürzeren Seite d eines der beiden gleichen neu
entstandenen Blätter sein: a / b = c / d
Außerdem ist die Seite c identisch mit der Seite b und wegen des Durchschneidens ist die Seite d genau halb so lang wie
die Seite a. Somit ist c = b und d = a/2 und es gilt die Beziehung: a / b = b / (a/2)
Umgeformt ergibt sich: a2 = 2 · b2
Die Seite a ist dann: a = b · √2
Und für die Seite b gilt: b = a / √2
Das Verhältnis x von kürzerer zu längerer Seite ist demnach: x = b / a = 1 : √2 = 1 : 1,414214
Die Seite a ist also um den Faktor √2 länger als die kürzere Seite. Schneidet man die beiden entstandenen Blätter
in gleicher Weise durch, bekommt man immer kleinere ähnliche Blätter, die sich vom jeweiligen vorherigen Blatt
um einen Faktor √2 in den Seitenlängen unterscheiden. Schließlich besitzt man lauter
gleiche Blätter, die dem Ausgangsblatt ähnlich sind. Schneidet man jedoch von den jeweils
entstehenden beiden Blättern nur eines durch, bekommt man eine unendliche Serie von immer kleiner werdenden
gleichzeitig vorhandenen Blättern, die alle einander ähnlich sind. Jeder einzelne Schnitt erzeugt also ein neues ähnliches
Blatt, wie man aus der folgenden Abbildung erkennt:
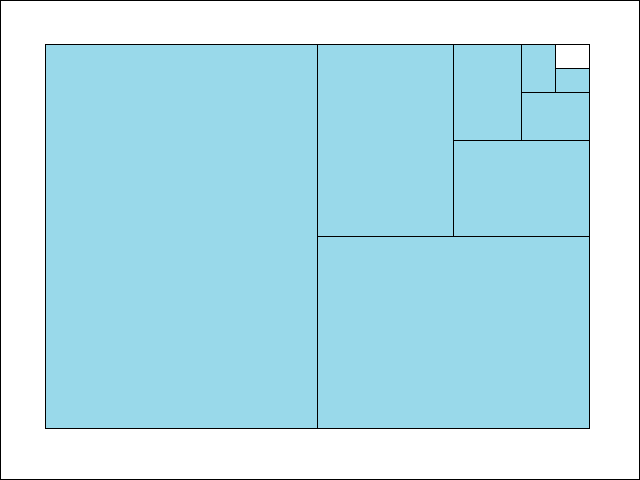
Legt man noch zusätzlich die Fläche des Ausgangsblattes mit
FDIN-A0 = a · b = 1 m2 fest, hat man ein sogenanntes DIN-A0-Blatt definiert,
von dem ausgehend alle weiteren DIN-Blätter hergestellt werden können. Die Länge der Seiten a und b
eines DIN-A0-Blattes errechnet man dadurch, dass man in der Gleichung für
FDIN-A0 die Seitenlänge b durch a / √2 ersetzt:
FDIN-A0 = a · a / √2 = 1 m2
Dann ist: a2 = √2 m2
Die Länge von a beträgt also: a = √(√2) m = 1,189207 m
Für die Seite b gilt dann: b = a / √2 = 1 / √(√2) m = 0,840896 m
Die folgende Tabelle enthält für die 8 größten DIN-A-Blätter die Seitenlängen und Flächen, die
sich ergeben, wenn man mathematisch exakt rechnet. Nach DIN werden allerdings diese genauen Werte
auf ganze Millimeter gerundet:
| kürzere Seite | längere Seite | Fläche |
| | | | |
| DIN A0 (Ausgangsblatt) | 0,840896 m | 1,189207 m | 1,000000 m2 |
| DIN A1 | 0,594604 m | 0,840896 m | 0,500000 m2 |
| DIN A2 | 0,420448 m | 0,594604 m | 0,250000 m2 |
| DIN A3 | 0,297302 m | 0,420448 m | 0,125000 m2 |
| DIN A4 | 0,210224 m | 0,297302 m | 0,062500 m2 |
| DIN A5 | 0,148651 m | 0,210224 m | 0,031250 m2 |
| DIN A6 | 0,105112 m | 0,148651 m | 0,015625 m2 |
| DIN A7 | 0,074325 m | 0,105112 m | 0,007812 m2 |
Für die Umschlagformate DIN-B0 und DIN-C0 gelten die gleichen Überlegungen, nur die Flächen sind anders definiert:
FDIN-B0 = √2 m2 = 1,4142 m2
FDIN-C0 = √(√2) m2 = 1,1892 m2
Wenn man als Ausgangsblatt ein DIN-Blatt verwendet, kann man also eine unendliche Serie von immer kleiner werdenden DIN-Blättern bekommen, wenn
man es immer weiter in der Mitte durchschneidet.
Goldene Rechtecke (Rechtecke nach dem Goldenen Schnitt)
Es gibt noch eine zweite Möglichkeit, durch Abschneiden mit jeweils nur einem Schnitt eine unendliche Serie
von immer kleiner werdenden und gleichzeitig vorhandenen einander ähnlichen Blättern zu erzeugen, bei denen die Länge der kürzeren Seite
eines Blattes gleich der Länge der längeren Seite des nächst kleineren Blattes ist. Allerdings muss man die Bedingung aufgeben, dass
der Schnitt in der Mitte des jeweiligen Blattes zu erfolgen hat. Die neue Serie von Blättern entsteht vielmehr dadurch, dass jeweils
ein Goldener Schnitt ausgeführt wird. Das Verhältnis x der kürzeren Seite b zur längeren Seite a der dabei entstehenden goldenen
Rechtecke ist gleich dem Verhältnis der größeren Seite zur Summe aus kürzerer und längerer Seite:
x = b / a = a / (a + b)
Umgeformt: (b / a) · (a + b) / a = 1
Weiter umgeformt: (b / a) · (b / a + 1) = 1
Also gilt: x · (x + 1) = 1
Umgeformt: x2 + x = 1
Die Lösung dieser quadratischen Gleichung ergibt das Seitenverhältnis der Blätter:
x = b / a = 1 : (½ + ½·√5) = 1 : 1,618034
Wie man aus den beiden Abbildungen erkennt, besitzt so ein Goldenes Rechteck ein deutlich anderes Seitenverhältnis als ein
DIN-Rechteck:
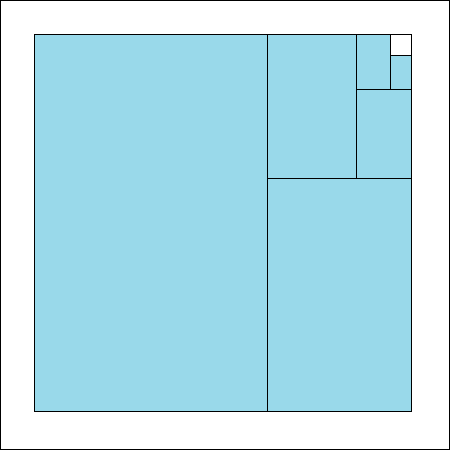
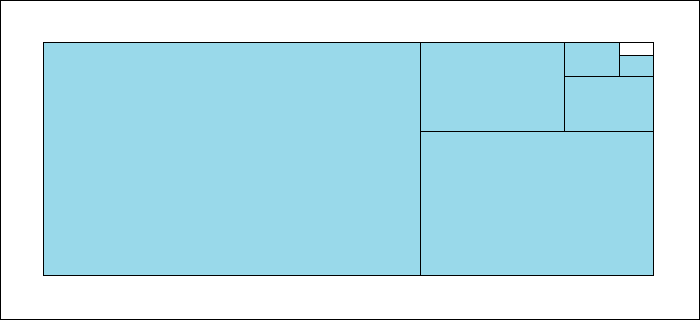
Man sieht außerdem, dass die Form des Ausgangsblattes hier weder ein DIN-Rechteck noch ein Goldenes Rechteck ist, sondern entweder ein Quadrat oder ein Rechteck
mit einem Seitenverhältnis von 1 : (1 + ½ + ½·√5) = 1 : 2,618034 = 1 : (½ + ½·√5)2 = 1 : 1,6180342, also mit einem Seitenverhältnis,
das dem Quadrat des Goldenen Schnitts entspricht. Nimmt man als Ausgangsblatt ein Quadrat, entsteht nach Abschneiden eines Goldenen Rechtecks ein Blatt mit dem Seitenverhältnis
von 1 : 1,6180342. Schneidet man von diesem Blatt wieder ein Goldenes Rechteck ab, bleibt wieder ein Quadrat übrig usw.. Nimmt man dagegen als Ausgangsblatt ein Rechteck
mit dem Seitenverhältnis 1 : 1,6180342, ist es genau umgekehrt. Die Form der Blätter, von denen die Goldenen Rechtecke abgeschnitten werden, wechselt also immer.
Legt man jeweils die Fläche der beiden Ausgangsblätter (wie beim DIN-A0-Blatt) mit 1 m2 fest, so sind beim Quadrat natürlich beide Seiten jeweils 1 m lang,
während beim zweiten Ausgangsblatt (Rechteck) für die beiden Seiten a und b gilt:
a = ( ½ + ½·√5) m = 1,618034 m
b = (-½ + ½·√5) m = 0,618034 m
Die folgende Tabelle enthält die beiden Ausgangsblätter und die daraus durch den Goldenen Schnitt
entstehenden 6 größten Goldenen Rechtecke (G1 bis G6):
| kürzere Seite | längere Seite | Fläche |
| | | | |
| Quadrat (Ausgangsblatt 1) | 1,000000 m | 1,000000 m | 1,000000 m2 |
| Rechteck (Ausgangsblatt 2) | 0,618034 m | 1,618034 m | 1,000000 m2 |
| G1 | 0,618034 m | 1,000000 m | 0,618034 m2 |
| G2 | 0,381966 m | 0,618034 m | 0,236068 m2 |
| G3 | 0,236068 m | 0,381966 m | 0,090170 m2 |
| G4 | 0,145898 m | 0,236068 m | 0,034442 m2 |
| G5 | 0,090170 m | 0,145898 m | 0,013156 m2 |
| G6 | 0,055728 m | 0,090170 m | 0,005025 m2 |
Weitere Möglichkeiten, eine unendliche Serie von immer kleiner werdenden einander ähnlichen Blättern
mit jeweils nur einem Schnitt zu erzeugen, die den obigen Bedingungen genügen, gibt es nicht.
Beweis: Die folgenden nicht maßstäblichen Zeichnungen zeigen, wie man von einem rechteckigen Ausgangsblatt die ersten beiden Blätter
einer jeweiligen Serie abschneiden kann. Es gibt nur 4 mögliche Fälle. Um die Orientierung dieser Blätter zu veranschaulichen, sind jeweils
Pfeile parallel zu den längeren Seiten dieser Blätter eingefügt. Die Seitenlängen sind ebenfalls aufgenommen. Ohne Beschränkung der
Allgemeinheit hat die längere Seite des ersten Blattes die Länge 1. x bezeichnet eine reelle Zahl kleiner als 1 und größer als 0.
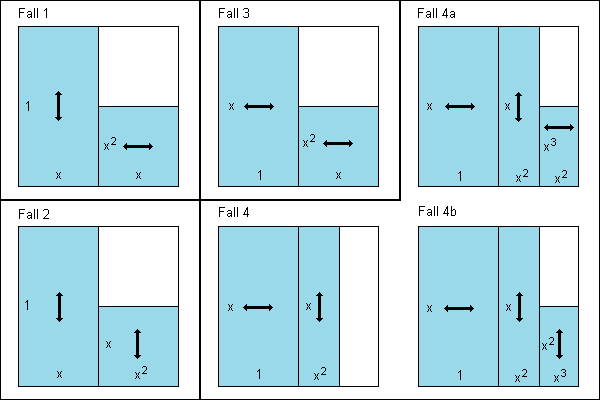
Wie man erkennt, liegen in den ersten 3 Fällen auch schon die Abmessungen der Ausgangsblätter fest. Im Fall 4 muss man noch
die beiden Möglichkeiten zum Abschneiden des dritten Blattes der jeweiligen Serie berücksichtigen, um die Abmessungen des
jeweiligen Ausgangsblattes festlegen zu können. Insgesamt gibt es also nur 5 Möglichkeiten, die Abmessungen und damit
auch die Flächen der Ausgangsblätter festzulegen. Die Gesamtfläche aller Blätter einer Serie liegt ebenfalls fest. Sie beträgt
(1 · x) + (x · x2) + (x2 · x3) + ...
= x + x3 + x5 + ... = x · (1 + x2 + x4 + ...) = x / (1 – x2)
Da diese Gesamtfläche mit der Fläche des jeweiligen Ausgangsrechtecks übereinstimmen muss, ergeben sich 5 Gleichungen, die zu maximal
5 möglichen Serien führen können:
Fall 1: x / (1 – x2) = 1 · (x + x); x2 = 1/2 (x = Seitenverhältnis der DIN-Blätter)
Fall 2: x / (1 – x2) = 1 · (x2 + x); x2 + x – 1 = 0 (x = Seitenverhältnis des Goldenen Rechtecks)
Fall 3: x / (1 – x2) = x · (x + 1); x2 + x – 1 = 0 (x = Seitenverhältnis des Goldenen Rechtecks)
Fall 4a: x / (1 – x2) = x · (x2 + x2 + 1); x2 = 1/2 (x = Seitenverhältnis der DIN-Blätter)
Fall 4b: x / (1 – x2) = x · (x3 + x2 + 1); x2 + x – 1 = 0 (x = Seitenverhältnis des Goldenen
Rechtecks)
Wie man sieht, sind nur 2 Serien möglich. Die eine Serie würde aus Blättern mit dem Seitenverhältnis der DIN-Blätter, die andere
Serie aus Goldenen Rechtecken bestehen. Wie oben gezeigt, lassen sich diese beiden Serien tatsächlich realisieren.
Hier sei noch eine interessante Frage erwähnt. Kann man auf einem DIN-Papier ein Bild in Form eines Goldenen Rechtecks so platzieren,
dass gleichzeitig ein überall gleich breiter Rand bleibt? Das ist tatsächlich möglich. Bei einem DIN-A4-Papier beispielsweise muss man
einen Rand mit einer Breite von 1/32 · √(√2) · (√18 + √10 – √20 – 2) m = 3,4665 cm freilassen.
Das Bild ist dann 22,7972 cm hoch und 14,0894 cm breit und besitzt das Seitenverhältnis des Goldenen Schnitts.
Weitere mögliche Rechtecke
Wenn allerdings die Blätter einer Serie auch durch mehr als einen Schnitt vom Ausgangsblatt abgetrennt werden dürfen,
dann gibt es mindestens noch zwei weitere Möglichkeiten. Bei der ersten Möglichkeit haben die Blätter der Serie ein
Seitenverhältnis x von 1 : √(½ + ½·√5) = 1 : 1,272020.
Das entspricht der Lösung der Gleichung x4 + x2 = 1 und ist gleich der Wurzel aus dem Goldenen Schnitt.
In der dargestellten Abbildung hat das Ausgangsblatt ebenfalls das Seitenverhältnis von 1 : 1,272020.
Allerdings kann man auch ein rechteckiges Blatt mit einem Seitenverhältnis x von 1 : √(11/2 + 5/2·√5) = 1 : 3,330191
als Ausgangsblatt verwenden.
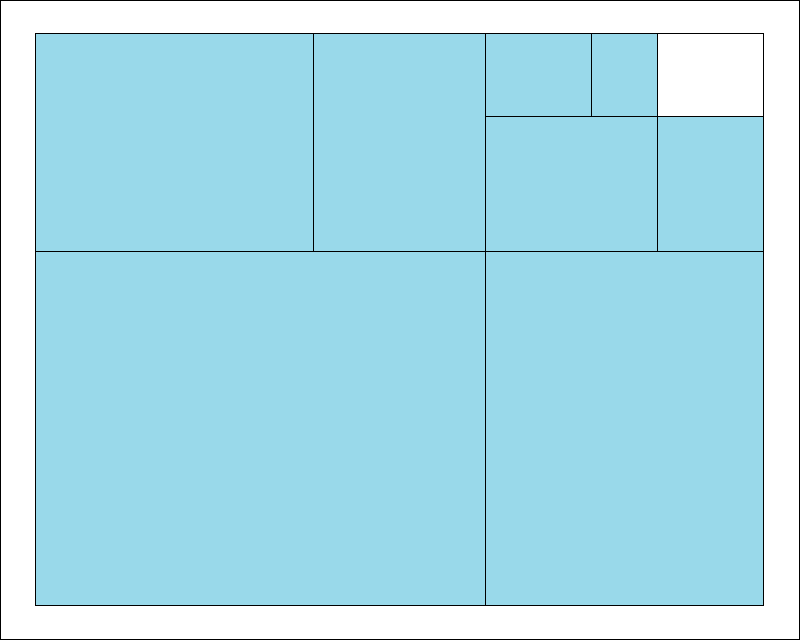
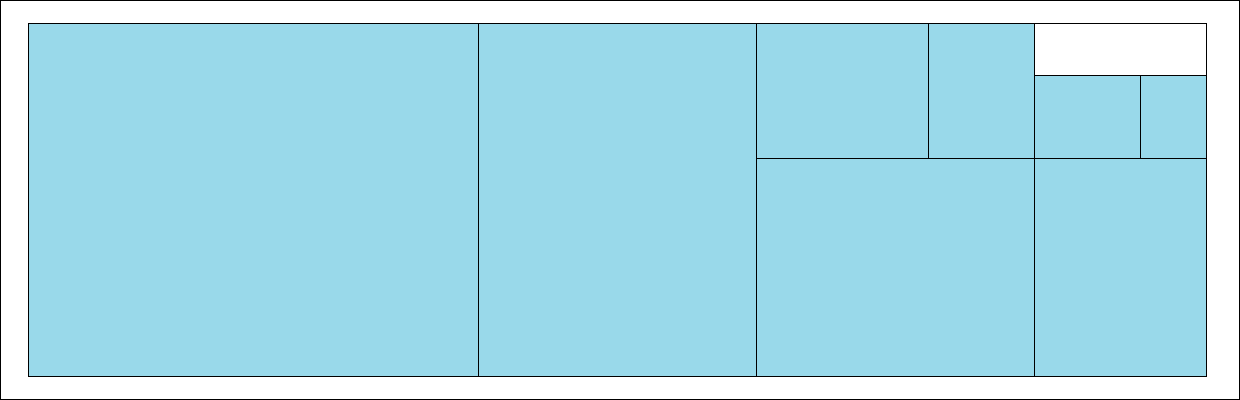
Die zweite Möglichkeit ergibt ein Seitenverhältnis x von 1 : 1,130685 für die Blätter
der Serie.
Dies entspricht der Lösung der Gleichung x6 + x4 + x3 – x2 = 1.
Die letzte Abbildung zeigt eine solche Serie, wobei ein rechteckiges Ausgangsblatt immer ein Seitenverhältnis von 1 : 1,278449 hat.
Das entspricht dem Quadrat der Seitenverhältnisse der abgetrennten Blätter.

Endliche Serie einander ähnlicher Rechtecke
Kann man von einem rechteckigen Ausgangsblatt mit jeweils nur einem Schnitt auch eine endliche Serie
von immer kleiner werdenden einander ähnlichen Blättern erzeugen, bei denen die Länge der kürzeren Seite eines Blattes gleich der Länge
der längeren Seite des nächst kleineren Blattes ist? Das ist tatsächlich möglich.
Für eine Serie von 2 einander ähnlichen Blättern gibt es sogar unendlich viele Möglichkeiten. Man kann immer 2 ähnliche Blätter, bei denen die
kleinere Seite des größeren Blattes gleich der größeren Seite des kleineren Blattes ist, zu einem rechteckigen Ausgangsblatt zusammensetzen.
Wenn das größere Blatt nämlich die Seiten a und b besitzt (a > b), dann hat das kleinere Blatt die Seiten b und b2 / a. Diese beiden
Blätter lassen sich immer zu einem Ausgangsblatt mit der längeren Seite a + b2 / a und der kürzeren Seite b zusammensetzen. Das
Seitenverhältnis des Ausgangsblattes ist dann b : (a + b2 / a) oder 1 : (a / b + b / a). Wird a sehr groß verglichen mit b, ist das
Seitenverhältnis des Ausgangsblattes fast gleich mit dem Seitenverhältnis der beiden ähnlichen Blätter. Auf der anderen Seite kann a höchstens
so klein werden wie b. Das Seitenverhältnis der beiden ähnlichen Blätter ist dann 1 : 1 und es handelt sich um zwei gleich große Quadrate.
Das Seitenverhältnis des Ausgangsblattes ist in diesem Fall gleich 1 : 2 oder gleich 0,5. Größer als 0,5 kann es nicht werden.
Für eine Serie von 3 Blättern gibt es allerdings nur eine Möglichkeit. Dabei haben die 3 Blätter der Serie ein Seitenverhältnis von 1 : 1,465571.
Das entspricht der Lösung der Gleichung x3 + x = 1. Das Ausgangsblatt hat aber ein anderes Seitenverhältnis, nämlich 1 : 1,147899.
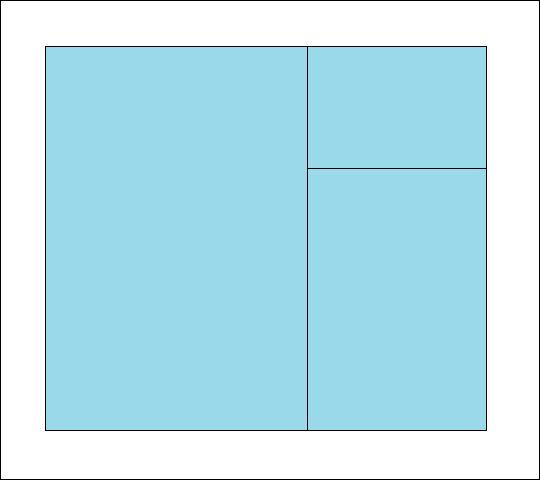
Für eine Serie von 4 Blättern gibt es ebenfalls nur eine Möglichkeit. Dabei haben die 4 Blätter wie bei der Serie
von 3 Blättern ein Seitenverhältnis von 1 : 1,465571. Das entspricht also ebenfalls der Lösung der Gleichung x3 + x = 1.
Das Ausgangsblatt hat hingegen ein Seitenverhältnis von 1 : 2,613470.
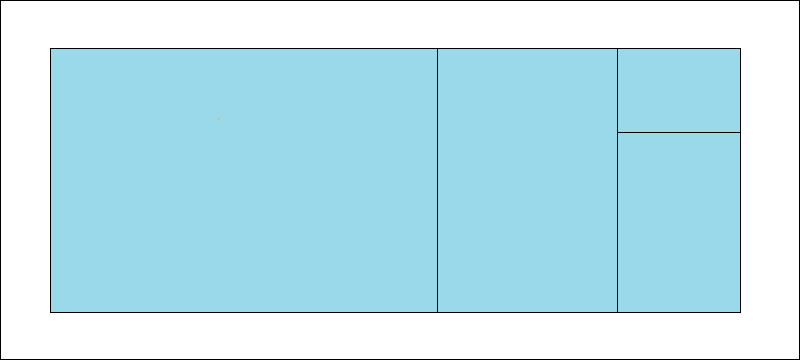
Für eine Serie von 5 Blättern gibt es keine Lösung mehr. Das kann man durch Fallunterscheidung zeigen. Das bedeutet
zugleich, dass es auch für mehr als 5 Blätter keine Lösung mehr geben kann, weil man dann durch Abschneiden mit jeweils einem Schnitt
auf eine Lösung mit jeweils einem Blatt weniger stoßen würde, also auch auf eine Lösung mit 5 Blättern.
Goldene Quader (Quader nach dem Goldenen Schnitt)
Die Überlegungen kann man auch auf den dreidimensionalen Fall übertragen. Gesucht wird hier
ein Quader, von dem man mit jeweils einem Schnitt eine Serie von immer kleiner werdenden einander ähnlichen Quadern abschneiden kann,
bei denen die kleinste Fläche gleich der größten Fläche des nächst kleineren Quaders ist. Dazu muss das Verhältnis der kürzesten
zur mittleren Seite gleich dem Verhältnis der mittleren zur längsten Seite sein. Als einzige Lösung ergeben sich Quader, deren
Seitenverhältnisse 1 : (dritte Wurzel aus 2) = 1 : 1,259921 betragen.
Wie bei den DIN-Blättern erfolgt der Schnitt auch bei den Quadern immer durch die Mitte der längsten Seiten.
Man könnte deshalb hier auch von "DIN"-Quadern sprechen. Bemerkenswerterweise hat auch der Ausgangsquader die gleichen Seitenverhältnisse.
Dagegen ist ein Goldener Quader, der sich dadurch auszeichnet, dass sowohl das Verhältnis von kürzester zu mittlerer als auch von
mittlerer zu längster Seite dem Verhältnis des Goldenen Schnitts entspricht, keine Lösung für den dreidimensionalen Fall.
Ein Goldener Quader erfüllt die geforderten Bedingungen nicht.
Links zum Thema:
Jürgen Köller: Papierformat A4
Copyright © Werner Brefeld (2005; Originalquelle)









