12. In einem Quadrat mit der Seitenlänge 4 befindet sich in jeder Ecke ein Kreis
mit dem Radius 1. Im Zentrum des Quadrates ist ein weiterer Kreis, der die anderen vier berührt.
Analog befände sich im dreidimensionalen Fall im Zentrum eines Würfels der Kantenlänge 4 eine Kugel,
die acht in den Ecken des Würfels platzierte Kugeln mit Radius 1 berühren würde. In welcher Dimension
wird die zentrale Hyperkugel so groß, dass sie alle Seitenflächen des Hyperwürfels berührt?
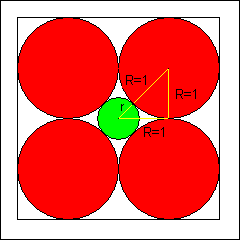
Bezeichnet man im zweidimensionalen Fall den Radius der Kreise in den Ecken mit R und den Radius des zentralen Kreises
mit r, dann gilt nach dem Satz des Pythagoras:
(r + R)2 = R2 + R2 = 2 · R2
r = R · √2 – R
Wegen R = 1 ist dann:
r = √2 – 1
Wendet man den Satz des Pythagoras noch einmal an, erhält man den Radius der zentralen Kugel im dreidimensionalen Fall:
(r + R)2 = R2 + R2 + R2 = 3 · R2
r = √3 – 1
Diese Überlegungen kann man entsprechend auf den n-dimensionalen Raum übertragen. Für den Radius der zentralen Hyperkugel
ergibt sich dann nach die folgende Formel:
r = √n – 1
Im vierdimensionalen Raum (n = 4) hat die zentrale Hyperkugel demnach den Radius r = 1. Sie ist damit genau so groß wie die 16 Hyperkugeln
in den Ecken des vierdimensionalen Hyperwürfels.
Das Zentrums des Hyperwürfels hat immer den Abstand d = 2 von der Mitte seiner begrenzenden 2·n "Seitenflächen", die
jeweils aus (n–1)-dimensionalen Hyperwürfeln bestehen. Die zentrale Hyperkugel berührt also diese "Seitenflächen“ des Hyperwürfels,
wenn ihr Radius r = 2 ist.
Das ist der Fall, wenn n = 9 ist.
Die neundimensionale zentrale Hyperkugel berührt also alle 18 begrenzenden "Seitenflächen" (achtdimensionalen Hyperwürfel)
des neundimensionalen Hyperwürfels. Im zehndimensionalen Raum liegen sogar Teile der zentralen Hyperkugel außerhalb des
zehndimensionalen Hyperwürfels. Je höher die Dimensionen werden, desto mehr verstärkt sich dieser Effekt.
Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, dass eine solche zentrale Hyperkugel
niemals die Seitenflächen des entsprechenden Hyperwürfels berühren oder gar durchdringen würde, weil sie im
zweidimensionalen Fall ja völlig und im dreidimensionalen Fall sehr gut eingesperrt sei. Die Intuition erkennt nicht,
dass sich da ein Trend anbahnt, der nicht vor den "Seitenflächen" endet.
Copyright © Werner Brefeld (2005)

