 |
Abdeckung einer Kreisscheibe
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
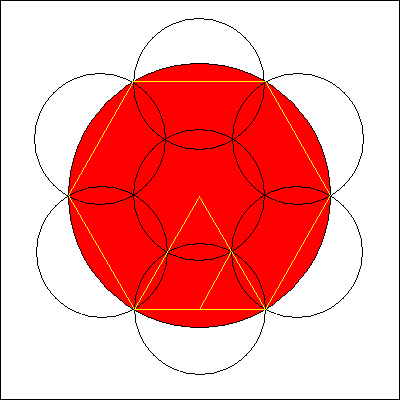
1. Gegeben sei eine Kreisscheibe. Wie viele Kreisscheiben mit dem halben Durchmesser braucht
man mindestens, um die große Scheibe vollständig abzudecken?
Wenn man der großen Kreisscheibe ein regelmäßiges Sechseck einbeschreibt, dann ist die Seitenlänge
dieses Sechsecks gleich dem Radius der Kreisscheibe. Die sechs Ecken dieses Sechsecks unterteilen den Rand der Kreisscheibe
in sechs gleiche Kreisbögen. Um diese Kreisbögen und damit den ganzen Rand abzudecken, benötigt man sechs Kreisscheiben mit
dem halben Durchmesser, deren Mittelpunkte auf den Seitenmitten des Sechsecks liegen. Diese sechs kleinen Kreisscheiben
decken allerdings nicht den Mittelpunkt der großen Kreisscheibe ab. Dazu benötigt man eine siebte zentral gelegene Kreisscheibe
mit einem Radius, der mindestens bis zum innen gelegenen Schnittpunkt der Ränder zweier benachbarter kleiner Kreisscheiben reichen
muss.
Um den benötigten Radius zu bestimmen, teilt man das regelmäßige Sechseck in sechs gleichseitige Dreiecke auf, wobei jeweils
eine der drei Dreieckseiten mit einer Sechseckseite identisch ist. Die eben erwähnten Schnittpunkte der Ränder liegen auf
den übrigen Dreieckseiten. Ein solcher Schnittpunkt bildet mit dem Mittelpunkt und einem Endpunkt einer benachbarten
Sechseckseite ein kleines Dreieck, welches nach Konstruktion zwei gleich lange Seiten und einen Innenwinkel von 60° besitzt.
Deshalb handelt es sich ebenfalls um ein gleichseitiges Dreieck. Die Seitenlänge ist gleich dem Radius einer kleinen Kreisscheibe.
Daraus folgt, dass sich die innen gelegenen Schnittpunkte der Ränder der kleinen Kreisscheiben genau auf einer Seitenmitte eines
der sechs großen Dreiecke befinden. Eine siebte zentral gelegene kleine Kreisscheibe reicht also gerade aus, um den Rest
der großen Kreisscheibe abzudecken.
Es sind also 7 Kreisscheiben mit dem halben Durchmesser nötig, um gerade die große Kreisscheibe abdecken zu können.
Da eine kleine Kreisscheibe niemals gleichzeitig den Mittelpunkt und endliche Teile des Randes der großen Kreisscheibe
abdecken kann, ist die gefundene Lösung auch die einzig mögliche.
Was ist verblüffend an diesem Mathematik-Rätsel? Da die große Kreisscheibe die vierfache Fläche einer
kleinen Kreisscheibe besitzt, glauben viele intuitiv, dass man fünf oder höchstens sechs, aber nicht sieben kleine
Kreisscheiben brauche, um die große Kreisscheibe abzudecken.
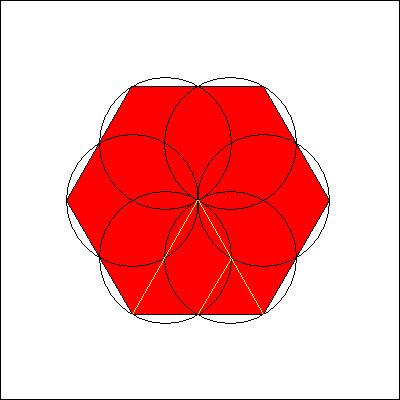
Ein Sechseck kann dagegen schon mit sechs Kreisscheiben, deren Radius halb so groß wie eine Sechseckseite ist, abgedeckt
werden. Dazu unterteilt man das Sechseck wieder in sechs gleichseitige Dreiecke und platziert die Mittelpunkte der
kleinen Kreisscheiben auf die Mitten der Dreieckseiten, die nicht mit den Sechseckseiten identisch sind. Diese Kreisscheiben
decken jeweils gerade den Mittelpunkt der großen Kreisscheibe ab. Dass sie zusätzlich jeweils genau die Hälfte von
zwei benachbarten Sechseckseiten abdecken, kann mit entsprechenden Argumenten wie oben gezeigt werden.
Copyright © Werner Brefeld (2005)


