 |
Mathematik im Alltag (nützliche Beispiele)
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
Wie viel Mathematik sollte jeder können, damit er im Alltag keine Nachteile hat? Welches sind die wichtigsten
Mathematikaufgaben, die man zur Bewältigung des Alltags beherrschen sollte? (Beispiele zu: Dreisatzrechnung, Prozentrechnung, Zinsrechnung,
Zinseszinsrechnung, Rentenrechnung, Flächenberechnung, Entscheidungsstrategie)
Wichtige Vorbemerkungen (Prozentangaben, Brüche, Abschätzungen)
Alle Aufgaben können mit einem einfachen Taschenrechner gelöst werden. Nur die letzte Aufgabe benötigt eine Wurzeltaste.
Eine Prozenttaste wird nicht gebraucht. Einige Rechnungen gehen mit einem Taschenrechner mit Potenztaste einfacher.
Damit man die Prozenttaste nicht benötigt, muss man sich klarmachen, dass eine Prozentangabe nichts anderes darstellt als eine normale Dezimalzahl.
Da Prozent "von Hundert" bedeutet, ist beispielsweise 75% gleich 75/100 oder gleich 0,75. Genauso bedeutet Promille "von Tausend".
10 Promille sind also gleich 1%. Hier sind einige Beispiele:
300% ist gleich 300/100 oder gleich 3
100% ist 1000 Promille oder gleich 1
28,4% ist gleich 0,284
10% ist gleich 0,1
3% ist gleich 0,03
1,37% ist gleich 0,0137
3 Promille ist gleich 3/1000 oder gleich 0,003
1,2 Promille ist gleich 0,12% oder gleich 0,0012
Will man nun zum Beispiel 19% von 850€ ausrechnen, muss man nur 0,19 mit 850 multiplizieren
und erhält als Ergebnis 0,19 · 850€ = 161,50€. Will man wissen, welcher Betrag sich ergibt,
wenn sich 850€ um 19% erhöhen, muss man 100% (die den 850€ entsprechen) zu 19% addieren.
119% von 850€ sind dann 1,19 · 850€ = 1011,50€. Würde sich 850€ um 100% erhöhen, muss man entsprechend
zu den 100% (die den 850€ entsprechen) weitere 100% addieren. 200% von 850€ sind dann 2 · 850€ = 1700€.
Eine Verteuerung um 100% entspricht also einer Verdoppelung des Preises. Bei einer Preiserhöhung um
200% würde sich folglich der Preis verdreifachen.
Ebenso sollte man Brüche nach Möglichkeit in Dezimalzahlen umwandeln. Beispielsweise sind 3/8
gleich 3 geteilt durch 8, und das sind 0,375. Ebenso ist 1/5 gleich 0,2, 7/10 sind gleich 0,7
und 4/9 sind ungefähr gleich 0,444444.
Die meisten Rechnungen der folgenden Abschnitte wird man mit einem Taschenrechner durchführen.
Bei der Eingabe kann man jedoch die verschiedensten Fehler machen. Beispielsweise kann man eine
falsche Ziffer eintippen, man kann den Dezimalpunkt an die falsche Stelle setzen oder gar die
Additionstaste mit der Multiplikationstaste verwechseln. Um grobe Fehler sofort zu bemerken,
ist es deshalb wichtig, im Kopf eine grobe Abschätzung zu machen. Dazu werden die verwendeten
Zahlen stark gerundet und dann die Rechnung durchgeführt.
Ein Beispiel: 4,25 · 2,60 ist ungefähr gleich 4 · 3 = 12. Das richtige Ergebnis kann höchstens ungefähr
doppelt oder halb so groß sein wie dieses im Kopf abgeschätzte Ergebnis. Zeigt der Taschenrechner mehr als 24
oder weniger als 6 an, dann sind diese Werte höchstwahrscheinlich falsch.
Ein weiteres Beispiel: 670 · 86,98 ist ungefähr gleich 700 · 90. Hier rechnet man mit Hilfe
des kleinen Einmaleins 7 · 9 = 63 und hängt die drei vorhandenen Nullen (die zwei von der 700 und
die eine von der 90) hinten dran. Das abgeschätzte Ergebnis beträgt also 63000.
Und noch ein Beispiel: 0,19 · 850 ist ungefähr gleich 0,2 · 800 = 160. Hier bleiben
von den zwei Nullen hinter der Acht nur eine übrig, weil die 2 erst eine Stelle nach dem
Dezimalpunkt kommt.
Bei einer Divisionsaufgabe ist es nützlich, die erste Zahl eine Stelle genauer zu runden:
2499 / 41 ist ungefähr gleich 2500 / 40. Dann überlegt man, dass 25 / 4 ungefähr gleich 6 sind. Bei einer Division
muss die Zahl der Nullen im Nenner (hier die eine Null von 40) von der Zahl der Nullen im Zähler (hier die 2 Nullen
von 2500) abgezogen werden. Es bleibt also nur eine Null übrig. Die wird an die 6 angehängt und das abgeschätzte
Ergebnis beträgt damit 60.
Energieverbrauch, Energieeinsparung, Erhitzungszeit, Wärmeleistung, Stromsicherung, Zeitangaben (mehrfache Zweisatzrechnung)
Eine Kühlgefrierkombination hat eine mittlere Leistung von 30 Watt.
Wie viel Energie verbraucht sie pro Jahr und was kostet das bei einem Preis von 0,22€ pro Kilowattstunde (kWh)?
Pro Stunde verbraucht die Kühlgefrierkombination im Mittel 30 Wattstunden oder 30/1000 Kilowattstunden = 0,03 kWh.
Ein Tag hat 24 Stunden und ein Jahr ungefähr 365,25 · 24 Stunden = 8766 Stunden.
Pro Jahr verbraucht die Kühlgefrierkombination also 8766 · 0,03 kWh = 263 kWh.
Eine Kilowattstunde (kWh) kostet 0,22€.
263 kWh kosten dann 263 · 0,22€ = 57,86€.
Die jährliche Stromrechnung für die Kühlgefrierkombination beträgt demnach 57,86€.
Eine warmweiße LED-Lampe von 12 Watt ist ungefähr so hell wie eine Glühlampe von 60 Watt.
Die Lebensdauer der LED-Lampe beträgt etwa 25.000 Stunden, die der Glühlampe nur etwa 1000 Stunden.
Wie viel Stromkosten spart die LED-Lampe während ihrer Lebensdauer im Vergleich zu den sonst benötigten 25 Glühlampen,
wenn man einen Preis von 0,22€ pro Kilowattstunde (kWh) rechnet?
Eine LED-Lampe von 12 Watt verbraucht 48 Watt weniger als eine Glühlampe von 60 Watt.
Pro Stunde spart diese LED-Lampe also 48 Wattstunden oder 48 / 1000 Kilowattstunden = 0,048 kWh.
In 25000 Stunden spart diese LED-Lampe dann 25000 · 0,048 kWh = 1200 kWh.
Eine Kilowattstunde (kWh) kostet 0,22€.
1200 kWh kosten dann 1200 · 0,22€ = 264€.
Eine warmweiße LED-Lampe spart während ihrer Lebensdauer also 264€ Stromkosten.
Ein Wasserkocher hat eine Leistung von 2400 Watt und fasst 1,5 Liter Wasser. Wie lange dauert es,
um diese Wassermenge zum Kochen (100°C) zu bringen, wenn die Temperatur des Wassers am Anfang 12°C beträgt?
1,5 Liter Wasser entsprechen 1,5 kg oder 1500 g Wasser.
Um 1 g Wasser um 1°C zu erwärmen, braucht man eine Energie von 1 Kalorie (cal).
Um 1500 g Wasser um 1°C zu erwärmen, braucht man dann 1500 cal.
Um das Wasser von 12°C auf 100°C zu erwärmen, muss man seine Temperatur um 88°C erhöhen.
Um 1500 g Wasser um 88°C zu erwärmen, braucht man also eine Energie von 88 · 1500 cal = 132.000 cal.
1 cal ist gleich 4,187 Joule (J) und 1 Joule (J) ist gleich 1 Wattsekunde (Ws).
132.000 cal sind also gleich 132.000 · 4,187 Ws = 552.700 Ws.
Hätte der Wasserkocher nur 1 Watt, bräuchte er 552 700 s, um das Wasser zu Kochen zu bringen.
Ein Wasserkocher mit 2400 Watt braucht dafür aber nur 552.700 s / 2400 = 230 s = 3 min 50 s.
Da jedoch ein Teil der Energie an die Umgebung abgegeben und nicht zur Erwärmung des Wassers genutzt wird, verlängert sich diese Zeit noch.
Mit der Annahme von 20% Verlust, also 80% Wirkungsgrad, ergeben sich dann 230 s / 0,8 = 288 s = 4 min 48 s.
Ein Mensch verbraucht täglich etwa 2000 Kilokalorien (kcal) oder 2.000.000 Kalorien (cal).
Welche Wärmeleistung gibt dieser Mensch an die Umgebung ab?
1 cal ist gleich 4,187 Joule (J) und 1 Joule (J) ist gleich 1 Wattsekunde (Ws).
2.000.000 cal sind also gleich 2.000.000 · 4,187 J = 8.374.000 J = 8.374.000 Ws.
(Nebenbei: Ein Mensch verbraucht also täglich etwa 8374 kJ (Kilojoule).)
1 Tag besitzt aber genau 60 · 60 · 24 = 86.400 Sekunden.
8.374.000 Ws / Tag sind also 8.374.000 Ws / 86.400 s = 97 Ws/s = 97 Watt.
Ein durchschnittlicher Mensch gibt also etwa 97 Watt Wärmeleistung ab.
In einem Haushalt beträgt die Wechselspannung 230 Volt (V) (Standardnetzspannung) und ein einzelner Stromkreis ist meistens
mit einer Sicherung für 16 Ampere (A) abgesichert. Welche Leistung dürfen alle an diesem Stromkreis angeschlossenen Geräte zusammen höchstens haben,
damit die Sicherung den Stromkreis nicht abschaltet?
1 Volt (V) mal 1 Ampere (A) ist gleich 1 Watt (W).
230 Volt mal 16 Ampere sind dann gleich (230 · 16) Watt = 3680 Watt.
Alle Geräte zusammen dürfen also höchstens eine Leistung von 3680 Watt haben, damit die Sicherung nicht abschaltet.
Wie viele Minuten sind 1,88 Stunden (1,88h)?
Und wie viele Stunden sind 8 Stunden, 37 Minuten und 13 Sekunden (8h 37min 13s)?
Eine Stunde sind ja gleich 60 Minuten.
1,88h sind dann entsprechend 1,88 · 60min = 112,8min.
Eine Minute sind ja gleich 60 Sekunden.
0,8min sind dann gleich 0,8 · 60s = 48s.
1,88 Stunden sind also gleich 112 Minuten und 48 Sekunden.
Eine Stunde sind ja gleich 3600 Sekunden.
8h sind dann gleich 8 · 3600s = 28.800s.
37min sind 37 · 60s = 2220s.
8h 37min 13s sind also gleich 28.800s + 2220s + 13s = 31.033s.
Und 31.033s sind gleich 31.033/3600 Stunden = 8,6203h.
Also sind 8h 37min 13s gleich 8,6203h.
Warenangeboten, Dollar und Euro, Backrezepte und Kochrezepte (Dreisatzrechnung)
In einem Lebensmittelgeschäft kostet eine 375g-Packung 4,99€ und die entsprechende 500g-Packung 6,99€.
Wie viel kosten umgerechnet 375g aus der 500g-Packung? Welche Packung ist also kostengünstiger?
Zu Lösung dieser Aufgabe hilft die Dreisatzrechnung:
500g aus der großen Packung kosten 6,99€.
1g aus der großen Packung kostet 6,99€ / 500 = 0,01398€.
375g aus der großen Packung kosten dann gerundet 375 · 0,01398€ = 5,24€.
Die kleine Packung (4,99€) ist also kostengünstiger.
Angenommen, der Dollarkurs beträgt 1,3724 Dollar pro Euro. Wie viele Euro sind dann 920 Dollar?
Auch diese Aufgabe lässt sich mit der Dreisatzrechnung lösen:
1,3724$ kosten 1€.
1$ kostet 1€ / 1,3724 = 0,72865€.
920$ kosten 920 · 1€ / 1,3724 = 670,36€.
Die 920$ sind also 670,36€ wert (920$ / 1,3724$/€ = 670,36€).
In einem Rezept werden zum Backen 3/4 kg Mehl, 3/4 kg Zucker, 200ml Milch, 150g Butter und 5 Eier angegeben.
Es sind aber nur noch 3 Eier vorhanden. Wie viel Mehl, Zucker, Milch und Butter sollte man dann verwenden?
Vor der Dreisatzrechnung wandelt man die Brüche bei den Gewichtsangaben um:
3/4 kg sind gleich 0,75kg oder gleich 750g.
Zu 5 Eiern gehören also 750g Mehl, 750g Zucker, 200ml Milch und 150g Butter.
Zu 1 Ei gehören dann 750g Mehl / 5 = 150g Mehl, 750g Zucker / 5 = 150g Zucker,
200ml Milch / 5 = 40ml Milch und 150g Butter / 5 = 30g Butter.
Zu 3 Eiern gehören entsprechend 3 · 150g Mehl = 450g Mehl, 3 · 150g Zucker = 450g Zucker,
3 · 40ml Milch = 120ml Milch und 3 · 30g Butter = 90g Butter.
Man sollte also 450g Mehl, 450g Zucker, 120ml Milch und 90g Butter verwenden.
Rabatte, Mehrwertsteuer, Inflationsrate (Prozentrechnung)
Der Preis eines Autos hat sich in einem Jahr von 18.499€ auf 18.999€ verteuert.
Der Verkäufer behauptet, das entspräche ja nur in etwa der allgemeinen Inflationsrate von 1,8%.
Wie viel Prozent ist das Auto teurer geworden? Hat der Verkäufer die Wahrheit gesagt?
Das Auto ist um den Faktor 18.999€ / 18.499€ = 1,027 teurer geworden (gerundet).
Um die relative Verteuerung zu erhalten, nimmt man die Zahl 1,027 und zieht 1 (was 100% entspricht) davon ab.
Man erhält 0,027 oder 2,7%. Der Verkäufer hat also nicht die Wahrheit gesagt.
Das Auto ist deutlich teurer geworden, als der Inflationsrate (1,8%) entspricht.
Ein LED-Fernseher kostet inklusive 16% Mehrwertsteuer 1999€. Die Mehrwertsteuer steigt auf 19%.
Um wie viel Prozent wird der LED-Fernseher teurer und was würde er dann kosten? Der Verkäufer gewährt auf den neuen Verkaufspreis
ausnahmsweise 2,55% Rabatt und behauptet, mit dem Rabatt wäre das Gerät sogar billiger als vor der Steuererhöhung.
Was kostet der LED-Fernseher jetzt? Hat der Verkäufer Recht?
In den 1999€ stecken sowohl der Preis ohne Mehrwertsteuer (100%) als auch die Mehrwertsteuer (16%),
also zusammen 116%.
Um den Preis ohne Mehrwertsteuer zu berechnen, müssen die 1999€ durch 116% oder einfach durch 1,16 geteilt werden.
Das ergibt einen Preis (Netto-Verkaufspreis) von 1723,28€ (gerundet).
Auf diesen Preis kommt jetzt die neue Mehrwertsteuer von 19%.
Den neuen Preis von 2050,70€ (gerundet) bekommt man, indem man 119% von 1723,28€ berechnet, also 1,19 mit 1723,28€ multipliziert.
Die prozentuale Verteuerung erhält man wieder, indem man 2050,70€ durch 1999€ teilt
und von dem gerundeten Ergebnis (1,0259) eins subtrahiert.
Es ergeben sich demnach 0,0259 oder 2,59% Preiserhöhung durch die Erhöhung der Mehrwertsteuer von 16% auf 19%.
Der Verkäufer gewährt nun 2,55% Rabatt auf den neuen Verkaufspreis von 2050,70€.
Der Rabatt beträgt also 0,0255 · 2050,70€ = 52,29€ (gerundet).
Demnach beträgt der neue Verkaufspreis für den LED-Fernseher 2050,70€ – 52,29€ = 1998,41€.
Der Verkäufer hat also Recht. Der Preis ist tatsächlich etwas niedriger als am Anfang.
An dieser Stelle sei kurz der Unterschied zwischen Prozenten und Prozentpunkten erklärt.
Wenn der Mehrwertsteuersatz von 16% auf 19 % erhöht wird, dann steigt er um 3 Prozentpunkte, weil 19% minus 16% gleich 3% sind.
Den Anstieg des Mehrwertsteuersatzes in Prozent erhält man dagegen, indem man 19% durch 16% teilt und vom Ergebnis 1 subtrahiert:
19% / 16% – 1 = 1,1875 – 1 = 0,1875 = 18,75%. Der Mehrwertsteuersatz ist also um beachtliche 18,75% gestiegen.
Ein Handwerker nimmt einen Stundenlohn von 46 €.
Er schätzt, dass er für die Arbeit 8 Stunden braucht und dass die Nebenkosten (An- und Abfahrt, Material) 500 € betragen.
Alle Beträge sind ohne Mehrwertsteuer gemeint. Die Mehrwertsteuer beträgt 19%. Wie hoch wäre nach diesen Angaben die Handwerkerrechnung?
Eine Stunde kostet 46€. 8 Stunden kosten also 8 · 46€ = 368€.
Zusammen mit den Nebenkosten von 500€ sind das 868€.
Darauf kommt dann noch die Mehrwertsteuer von 19%.
Die Endsumme sind dann 119% von 868€ oder 1,19 · 868€ = 1032,92€.
So hoch würde die Handwerkerrechnung ausfallen.
Geldanlage (Zinsrechnung, Zinseszinsrechnung)
Die eine Bank gibt nach 7 Jahren einen einmaligen Bonus von 30% auf das zu Anfang eingezahlte Geld.
Bei der anderen Bank beträgt der Zinssatz auf einem Sparkonto 4,2% pro Jahr.
Wie viel Geld bekommt man jeweils nach 7 Jahren zurück, wenn man am Anfang 3000 € eingezahlt hat?
Den Bonus kann man als einmaligen Zins betrachten. Dafür gilt die einfache Zinsformel, weil dieser
einmalige Zins nicht wieder verzinst wird. Die Formel dafür lautet:
Endkapital = Anfangskapital · (1 + Zinssatz).
Es ergibt sich also: Endkapital = 3000€ · (1 + 30%) = 3000€ · (1 + 0,3) = 3000€ · 1,3 = 3900€.
Man bekommt nach 7 Jahren also 3900€ zurück.
Im zweiten Beispiel werden die Zinsen, die in jedem Jahr anfallen,
bis zum Ende der Laufzeit weiter verzinst. Hier gilt die Zinseszinsformel:
Endkapital = Anfangskapital · (1 + Zinssatz)(Anzahl der Jahre).
Hier ergibt sich: Endkapital = 3000€ · (1 + 4,2%)7 = 3000€ · (1 + 0,042)7.
Endkapital = 3000€ · 1,0427 = 3000€ · 1,33375 = 4001,25€ (gerundet).
Hat man keine Potenztaste, um 1,0427 zu berechnen, kann man auch 1,042 siebenmal
mit sich selbst malnehmen, was natürlich etwas mühseliger ist.
Man bekommt hier also nach 7 Jahren 4001,25€ zurück, mehr als im ersten Fall.
Jemand zahlt zu Anfang des Jahres 8000€ auf ein Sparbuch ein. Der Zinssatz beträgt 2,7% pro Jahr.
Nach 7 Monaten hebt er das eingezahlte Geld und die aufgelaufenen Zinsen ab. Wie viel kann er abheben?
Hier gilt wieder die einfache Zinsformel:
Endkapital = Anfangskapital · (1 + Zinssatz).
Weil das Geld jedoch nicht ein Jahr oder 12 Monate, sondern nur 7 Monate auf dem Konto war,
beträgt der Zinssatz für diesen Zeitraum nur 7/12 mal 2,7% oder 1,575%.
Es ergibt sich also: Endkapital = 8000€ · (1 + 1,575%) = 8000€ · (1 + 0,01575) = 8000€ · 1,01575 = 8126€.
Er kann also 8126€ abheben.
Ein Auto wurde vor 5 Jahren neu für 20.000€ gekauft. Der Wertverlust pro Jahr wird mit ungefähr 20% angenommen.
Wie viel ist das Auto jetzt noch ungefähr wert?
Hier wird wieder die Zinseszinsformel benötigt, wobei man den Wertverlust pro Jahr als
negativen Zins betrachten muss. Man muss also rechnen:
Endkapital = Anfangskapital · (1 + Zinssatz)(Anzahl der Jahre).
Es ergibt sich: Endkapital = 20.000€ · (1 – 20%)5 = 20.000€ · (1 – 0,2)5.
Endkapital = 20.000€ · 0,85 = 20.000€ · 0,32768 = 6553,60€.
Das Auto ist jetzt also nur noch ungefähr 6553,60€ wert.
Ratensparverträge, Geldleihe (Rentenrechnung)
Bei einem Sparvertrag wird am Anfang eines jeden Monats eine Rate von 50€ eingezahlt,
der Zinssatz beträgt 5% pro Jahr und die Laufzeit ist 20 Jahre. Die anfallenden Zinsen bleiben stehen und werden mitverzinst.
Wie viel Kapital hat sich am Ende der Laufzeit angesammelt?
Zur Berechnung wird die Formel für die Rentenrechnung benötigt. Sie lautet:
Endkapital = Anfangskapital · (1 + Zinssatz)(Anzahl der Jahre)
+ Ratenbetrag · ((1 + Zinssatz)(Anzahl der Jahre) – 1) / Zinssatz.
Der Ratenbetrag bezeichnet hier den jeweils am Jahresende eingezahlten Betrag. Der Betrag wird aber hier nicht
am Ende des Jahres gezahlt, sondern jeweils ein Zwölftel davon schon am Anfang der Monate dieses Jahres, also
zwischen 1 und 12 Monate früher. Diese Beträge erzielen im laufenden Jahr schon Zinsen, die dem
Sparbetrag hinzugerechnet werden müssen. Diese Zinsen entsprechen der Verzinsung von 50€ für insgesamt
(1+2+3+4+5+6+7+8+9+10+11+12) Monate. Das sind insgesamt 78 Monate oder 6,5 Jahre. Diese Zinsen betragen
also 6,5 · 5% · 50€ = 6,5 · 0,05 · 50€ = 16,25€. Der Sparbetrag ist also nicht 12 · 50€ = 600€ pro Jahr,
sondern 600€ + 16,25€ = 616,25€. Dieser Wert muss also genommen werden. Da zu Anfang kein Kapital
vorhanden ist, wird für das Anfangskapital 0€ eingesetzt:
Endkapital = 0€ · (1 + 5%)20 + 616,25€ · ((1 + 5%)20 – 1) / 5%.
Endkapital = 616,25€ · (1,0520 – 1) / 0,05.
Endkapital = 616,25€ · (2,653298 – 1) / 0,05.
Endkapital = 616,25€ · 33,06596 = 20.376,89€.
Nach 20 Jahren haben sich also 20.376,89€ angesammelt.
Ein Kunde leiht bei einer Kreditbank für den Kauf eines Hauses 100.000€. Am Ende eines jeden Jahres zahlt er 8400€ zurück.
Die Bank verlangt einen Leihzins von 6%. Wie groß sind die Schulden noch nach 20 Jahren? Welche Höhe der Schuld ergibt sich,
wenn der Kunde nicht erst am Ende jeden Jahres 8400€ zurückzahlt, sondern schon am Ende eines jeden Monats ein Zwölftel davon, also 700€?
Zur Berechnung wird wieder die Formel für die Rentenrechnung benötigt:
Endkapital = Anfangskapital · (1 + Zinssatz)(Anzahl der Jahre)
+ Ratenbetrag · ((1 + Zinssatz)(Anzahl der Jahre) – 1) / Zinssatz.
Das Anfangskapital ist hier negativ, weil es sich ja um Schulden handelt:
Endkapital = –100.000€ · (1 + 6%)20 + 8400€ · ((1 + 6%)20 – 1) / 6%.
Endkapital = –100.000€ · 1,0620 + 8400€ · (1,0620 – 1) / 0,06.
Endkapital = –100.000€ · 3,207135 + 8400€ · (3,207135 – 1) / 0,06.
Endkapital = –320.714€ + 308.999€ = –11.715€.
Es bleibt also eine Schuld von 11.715€ übrig.
Erfolgen die Rückzahlungen, so wie oben beschrieben, monatlich, dann werden die Beträge von jeweils 700€
bis zum Ende des Jahres zwischen 0 und 11 Monaten "verzinst". Auf das Jahresende bezogen müssen also Zinsen
addiert werden, die der Verzinsung von 700€ für insgesamt (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11) Monaten,
also 66 Monaten oder 5,5 Jahren entsprechen. Diese Zinsen betragen 5,5 · 6% · 700€ = 231€.
In diesem Falle zahlt man also nicht 8400€ pro Jahr, sondern 8400€ + 231€ = 8631€. Setzt man diesen Wert in die
obige Rechnung ein, so bleibt nach 20 Jahren eine Restschuld von 3218€.
Wände streichen, Tapeten kleben, Fliesen legen, Teppich legen, Mutterboden auffüllen
(Flächenberechnung eines Rechtecks, Volumenberechnung eines Quaders)
Eine Länge wird in Meter, eine Fläche in Quadratmeter und ein Volumen (Rauminhalt) in Kubikmeter gemessen. Meter,
Quadratmeter und Kubikmeter sind also verschiedene physikalische Einheiten, die man nicht miteinander vergleichen kann.
Fragen wie "Wie viel Meter sind ein Quadratmeter?" oder "Wie viel Quadratmeter sind ein Kubikmeter?" sind deshalb
genau sinnlos wie die Frage "Wie viel Sekunden sind ein Kilogramm?" oder "Wie viel Watt sind eine Kilowattstunde?".
Allerdings kann man aus Länge, Breite und Höhe, die in Metern gemessen werden, Flächen und Volumen berechnen.
Die Wände eines Raumes sollen gestrichen werden. Der Raum ist 2,60 Meter hoch. Zwei Wände sind 3,30 Meter breit.
Die Breite der anderen beiden Wände beträgt 4,25 Meter. Der Raum hat ein 1,40 Meter breites und 1,10 Meter hohes Fenster.
Die Tür ist 0,85 Meter breit und 2,00 Meter hoch. Wie groß ist die Fläche, die gestrichen werden muss?
Die Fläche von Wänden, Türen und Fenstern erhält man, indem man die Breite mit der Höhe multipliziert.
Die schmaleren Wände haben die Fläche 3,30 Meter · 2,60 Meter = 8,58 Quadratmeter.
Die breiteren Wände haben die Fläche 4,25 Meter · 2,60 Meter = 11,05 Quadratmeter.
Das Fenster hat die Fläche 1,40 Meter · 1,10 Meter = 1,54 Quadratmeter.
Die Tür hat die Fläche 0,85 Meter · 2,00 Meter = 1,70 Quadratmeter.
Die zu streichende Fläche ist also (8,58 + 8,58 + 11,05 + 11,05 – 1,54 – 1,70) Quadratmeter oder 36,02 Quadratmeter groß.
Ein Garten von 16 Meter Länge und 7 Meter Breite soll eine 20 cm dicke Schicht Mutterboden bekommen.
Wie viel Kubikmeter Mutterboden müssen besorgt werden?
Das Volumen bestimmt man in diesem Fall durch die Rechnung Länge mal Breite mal Höhe.
Da 20 cm gleich 0,2 Meter sind, müssen 16 Meter mal 7 Meter mal 0,2 Meter gleich 22,4 Kubikmeter besorgt werden.
Grundstücksfläche (Dreiecksflächenberechnung)
Jemand will ein Grundstück verkaufen. Es ist vorne 28m und hinten 22m breit. Links ist es 23m tief und rechts 17m.
Er sagt, das Grundstück sei ja im Mittel 25 Meter breit und 20 Meter tief, also 25 Meter mal 20 Meter gleich 500 Quadratmeter groß.
Da er für den Quadratmeter 400€ haben möchte, würde er das Grundstück für 200.000€ verkaufen. Sie haben ein ungutes Gefühl,
gehen zum Grundstück und messen die Strecken nach. Aber die Angaben stimmen. Zur Sicherheit messen Sie auch noch eine Diagonale
des viereckigen Grundstücks. Sie misst 31m. Wie groß ist das Grundstück wirklich und was dürfte es demnach kosten?
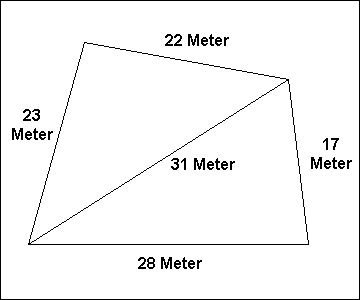
Wäre das Grundstück rechteckig, müsste man nur die Breite mit der Tiefe multiplizieren,
um die Fläche zu erhalten. Meist sind Grundstücke zwar viereckig, aber nicht rechtwinklig.
Von diesen Grundstücken mit einem Maßband die Länge aller 4 Seiten zu bestimmen, ist
zwar nicht besonders schwierig, reicht aber nicht. Man müsste mindestens noch den Winkel
an einer Ecke messen, wozu aber fast immer die Hilfsmittel fehlen. Ein eleganter Ausweg
ist die Messung einer Diagonale. Sie teilt das Viereck in zwei Dreiecke, deren Flächen
nun getrennt berechnet werden können.
Bezeichnet man die Seiten eines Dreiecks mit a, b und c, dann beträgt die Fläche F:
F = √( (a + b + c) · (a + b – c) · (a + c – b) · ( b + c – a) ) / 4
Setzt man für das linke Dreieck a = 22m, b = 23m und c = 31m, so erhält man:
F = √( (22m + 23m + 31m) · (22m + 23m – 31m) · (22m + 31m – 23m) · (23m + 31m – 22m) ) / 4
F = √(76m · 14m · 30m · 32m) / 4
F = √(1.021.440) Quadratmeter / 4 = 1010,66 Quadratmeter / 4 = 252,67 Quadratmeter (gerundet)
Genauso wird das rechte Dreieck berechnet. Setzt man hier a = 28m, b = 23m und c = 31m, so erhält man:
F = √( (17m + 31m + 28m) · (17m + 31m – 28m) · (17m + 28m – 31m) · (31m + 28m – 17m) ) / 4
F = √(76m · 20m · 14m · 42m) / 4 = 236,35 Quadratmeter
Die 252,67 Quadratmeter und die 236,35 Quadratmeter der beiden Dreiecke zusammen ergeben 489,02 Quadratmeter.
Bei 400€ pro Quadratmeter dürfte das Grundstück demnach nur 489,02 · 400€ = 195.608€ kosten.
Sie würden also 4392€ zu viel bezahlen, wenn Sie der obigen Behauptung glauben würden.
Hauskauf oder Arbeitsstellensuche (Entscheidungsstrategie)
(Originalquelle)
Im Leben gibt es gelegentlich Situationen, bei denen man sich für oder gegen etwas entscheiden muss, ohne gleichzeitig eine Alternative zu haben.
Bekommt man beispielsweise nach einem Vorstellungsgespräch eine Arbeitsstelle angeboten, muss man sich oft entscheiden, bevor man ein Angebot
für eine weitere Arbeitsstelle besitzt. Das Gleiche passiert oft, wenn man sich nach einer Besichtigung für den Kauf eines Hauses entscheiden muss,
bevor man die Gelegenheit zur Besichtigung eines weiteren Hauses besitzt. Gibt es für solche Situationen eine optimale Strategie?
Tatsächlich gibt es für dieses Problem eine optimale Lösung. Nimmt man den Hauskauf als Beispiel, dann muss das Ziel sein, im Durchschnitt
ein möglichst gutes Haus zu erwerben. Dabei muss jeder selbst entscheiden, was er unter "gut" oder "besser" versteht. Wichtig für die optimale Strategie ist,
dass man abschätzen kann, wie viele Häuser man maximal besichtigen würde, bevor man frustriert aufgäbe und in seiner momentanen Wohnung bliebe.
Außerdem ist für die Berechnung der optimalen Strategie wichtig, dass man jedes besichtigte Haus auch angeboten bekommt und notfalls auch erwerben würde.
Nach jeder Hausbesichtigung muss man dann alle bisher gesehenen Objekte in eine persönliche Favoritenreihenfolge bringen. Dabei käme der Top-Favorit auf Platz 1.
Die folgende Tabelle enthält die Informationen für die jeweils optimale Strategie. Angenommen, man glaubt, insgesamt 7 Häuser (Objekte) besichtigen zu können.
Dann ist die Zeile in der Tabelle wichtig, bei der links eine 7 steht. Die rechts davon stehenden Zahlen geben die Platzierung an, die für die Entscheidung
nach der ersten, zweiten, dritten, usw. Besichtigung (Gelegenheit) maßgeblich ist. In diesem Beispiel dürfte man das erste und zweite Haus nur besichtigen,
aber nicht kaufen, das dritte Haus würde man nehmen, wenn es von den drei besichtigten das Beste ist, das vierte würde man dann nehmen, wenn es von den vier
schon gesehenen das Beste ist, für das fünfte würde man sich entscheiden, wenn es mindestens auf Platz 2 kommt und für das sechste Haus würde Platz 3 reichen.
Wenn man schließlich auch noch das siebte Haus besichtigen müsste, ist man gezwungen, sich dafür entscheiden, denn es erreicht ja immer mindestens Platz 7.
| Objekte | G1 | G2 | G3 | G4 | G5 | G6 |
G7 | G8 | G9 | G10 | G11 | G12 | G13 |
G14 | G15 | G16 | mittlere Anzahl | mittlere Platzierung |
| | | | | | |
| | | | | | |
| | | der | (Erwartungswert) |
| | | | | | |
| | | | | | |
| | | Gelegenheiten | |
| | | | | | |
| | | | | | |
| | | | |
| | | | | | | | | | | | |
| | | | | |
| 1 | 1 | | | | | | | | | | | |
| | | | 1,000 | 1,000 |
| 2 | 1 | | | | | | | | | | | |
| | | | 1,000 | 1,500 |
| 3 | - | 1 | 3 | | | | | | | | | |
| | | | 2,500 | 1,667 |
| 4 | - | 1 | 2 | 4 | | | | | | | | |
| | | | 2,667 | 1,875 |
| 5 | - | 1 | 1 | 2 | 5 | | | | | | | |
| | | | 3,000 | 2,050 |
| 6 | - | - | 1 | 2 | 3 | 6 | | | | | | |
| | | | 4,133 | 2,217 |
| 7 | - | - | 1 | 1 | 2 | 3 | 7 | | | | | |
| | | | 4,617 | 2,276 |
| 8 | - | - | 1 | 1 | 2 | 2 | 4 | 8 | | | | |
| | | | 4,752 | 2,400 |
| 9 | - | - | - | 1 | 1 | 2 | 3 | 4 | 9 | | | |
| | | | 6,093 | 2,496 |
| 10 | - | - | - | 1 | 1 | 2 | 2 | 3 | 5 | 10 | | |
| | | | 6,294 | 2,558 |
| 11 | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 5 | 11 | |
| | | | 6,743 | 2,614 |
| 12 | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 6 | 12 |
| | | | 6,809 | 2,684 |
| 13 | - | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 6 |
13 | | | | 8,256 | 2,735 |
| 14 | - | - | - | - | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 5 |
7 | 14 | | | 8,348 | 2,783 |
| 15 | - | - | - | - | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 4 |
5 | 7 | 15 | | 8,754 | 2,818 |
| 16 | - | - | - | - | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 |
4 | 5 | 8 | 16 | 8,940 | 2,871 |
Die vorletzte Spalte gibt an, wie viele Häuser man durchschnittlich bis zum Kauf besichtigen musste (Zahl der Gelegenheiten).
Obwohl man glaubte, sich maximal 7 Besichtigungen zumuten zu können, braucht man in diesem Beispiel im Mittel nur 4,617 Besichtigungen bis zum Kauf.
Die letzte Spalte gibt schließlich an, welche Platzierung man im Durchschnitt für das ausgewählte Haus erwarten kann.
Bei maximal 7 besichtigten Häusern erreicht man also im Mittel Platz 2,276 von allen 7 Häusern. Dieser Wert berücksichtigt also nicht nur die besichtigten Häuser,
sondern auch diejenigen, die man sich nicht mehr anzuschauen brauchte, weil man schon vorher zugreifen konnte. Das ist also keine schlechte Platzierung.
Berechnungsverfahren: Ein Computer-Programm berechnet alle möglichen Favoritenreihenfolgen der möglichen Käufer. Bei z.B. 7 Häusern wären das
7! = 5040 verschiedene Reihenfolgen (Permutationen). Für Jede denkbare Strategie muss der Computer jeweils aus allen 5040 Permutationen
die mittlere Anzahl der Gelegenheiten und die mittlere Platzierung ermitteln.
Eine von vielen denkbaren Strategien wäre z.B. die folgende:
1. Haus: anschauen, aber nicht kaufen
2. Haus: kaufen, wenn auf Platz 1
3. Haus: kaufen, wenn auf Platz 1
4. Haus: kaufen, wenn mindestens auf Platz 3
5. Haus: kaufen, wenn mindestens auf Platz 3
6. Haus: kaufen, wenn mindestens auf Platz 5
7. Haus: kaufen, wenn mindestens auf Platz 7
Die optimale Strategie ist dann die mit der besten mittleren Platzierung (siehe Tabelle).
Ein zweites Berechnungsverfahren zur Berechnung der optimalen Strategie und der Erwartungswerte beruht darauf, dass man die Berechnungen von hinten nach vorne durchführt.
Beispielweise geht man von maximal 5 Häusern aus. Das fünfte Haus kann in der Favoritenliste mit jeweils gleicher Wahrscheinlichkeit auf Platz 1, 2, 3, 4 oder 5 stehen.
Der Erwartungswert der Platzierung ist also 3. Das vierte Haus sollte man also nur kaufen, wenn man damit den Erwartungswert von 3 (natürlich bezogen auf alle 5 Häuser) unterbietet.
Für die Entscheidung sucht man also die größte Platz-Nummer (in der Favoritenliste), mit der man der Wert von 3 gerade noch unterbietet.
Die Platz-Nummer 3 scheidet aus, weil Platz 3 unter 4 Häusern einen Erwartungswert von mehr als 3 ergibt (bezogen auf alle 5 Häuser).
Nimmt man als Entscheidungskriterium Platz 2, so bedeutet das, dass man in 50% der Fälle das Haus nicht kauft, weil sich Platz 3 oder 4 ergeben hat.
Entsprechend muss man hier das letzte Haus mit einem Erwartungswert von 3 kaufen. In 25% der Fälle hat man Platz 2.
Das ist aber nur in 60% der Fälle der echte Platz 2 (bezogen auf alle 5 Häuser), weil in 40% der Fälle das fünfte Haus auf Platz 1 oder 2 steht.
In diesen Fällen steht das vierte Haus nur auf Platz 3 (bezogen auf alle 5 Häuser).
Bei den restlichen 25% hat man Platz 1 geschafft. Das ist aber nur in 80% der Fälle der echte Platz 1 (bezogen auf alle 5 Häuser),
weil in 20% der Fälle das fünfte Haus auf Platz 1 steht. In diesen Fällen steht das vierte Haus nur auf Platz 2 (bezogen auf alle 5 Häuser).
Insgesamt erhält man bei dieser Strategie also einen Erwartungswert von 50% · 3 + 25% · (60% · 2 + 40% · 3) + 25% · (80% · 1 + 20% · 2) = 2,4
Da dieser Wert unter 3 liegt, muss es die richtige Strategie für die Entscheidung zum Kauf des vierten Hauses sein, Platz 2 als Entscheidungskriterium zu nehmen.
Entsprechend muss man nun die Überlegungen für das dritte, zweite und erste Haus durchführen. Am Schluss erhält man dann den richtigen Platzierungs-Erwartungswert für 5 Häuser.
Die hier beschriebene Entscheidungsstrategie ist eine Erweiterung der nicht ganz so realistischen Odds-Strategie. Bei der Odds-Strategie kommt es darauf an,
mit einer möglichst großen Wahrscheinlichkeit das beste Haus zu bekommen. Dabei wird eine bestimmte Zahl von Häuser nur besichtigt, aber nicht erworben. Danach kauft man
das erste Haus, dass unter den besichtigten Häusern die beste Platzierung (also Favoritenplatz 1) bekommen hat. Der Preis, den man bei der originalen Odds-Strategie zahlt,
ist die im Mittel schlechtere Platzierung des erworbenen Hauses. Für diese Strategie gilt die folgende Tabelle:
| Objekte | G1 | G2 | G3 | G4 | G5 | G6 |
G7 | G8 | G9 | G10 | G11 | G12 | |
| | | mittlere Anzahl | mittlere Platzierung |
| | | | | | |
| | | | | | |
| | | der | (Erwartungswert) |
| | | | | | |
| | | | | | |
| | | Gelegenheiten | |
| | | | | | |
| | | | | | |
| | | | |
| | | | | | | | | | | | |
| | | | | |
| 1 | 1 | | | | | | | | | | | |
| | | | 1,000 | 1,000 |
| 2 | 1 | | | | | | | | | | | |
| | | | 1,000 | 1,500 |
| 3 | - | 1 | 3 | | | | | | | | | |
| | | | 2,500 | 1,667 |
| 4 | - | 1 | 1 | 4 | | | | | | | | |
| | | | 2,833 | 1,875 |
| 5 | - | - | 1 | 1 | 5 | | | | | | | |
| | | | 4,167 | 2,200 |
| 6 | - | - | 1 | 1 | 1 | 6 | | | | | | |
| | | | 4,567 | 2,333 |
| 7 | - | - | 1 | 1 | 1 | 1 | 7 | | | | | |
| | | | 4,900 | 2,476 |
| 8 | - | - | - | 1 | 1 | 1 | 1 | 8 | | | | |
| | | | 6,279 | 2,812 |
| 9 | - | - | - | 1 | 1 | 1 | 1 | 1 | 9 | | | |
| | | | 6,654 | 2,917 |
| 10 | - | - | - | 1 | 1 | 1 | 1 | 1 | 1 | 10 | | |
| | | | 6,987 | 3,025 |
| 11 | - | - | - | - | 1 | 1 | 1 | 1 | 1 | 1 | 11 | |
| | | | 8,383 | 3,382 |
| 12 | - | - | - | - | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 12 |
| | | | 8,746 | 3,467 |
Copyright © Werner Brefeld (2007)

