Der Pythagorasbaum und seine Blätter Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum, Themenübersicht auf der Hauptseite: Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben

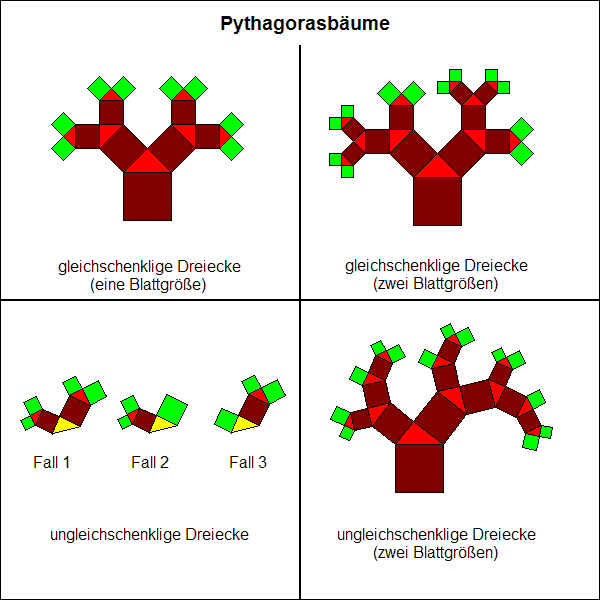
24. Ein Pythagorasbaum entsteht, wenn man auf ein Quadrat (Stamm) ein rechtwinkliges Dreieck (Verzweigung) mit seiner Hypotenuse aufsetzt. An die Katheten schließen sich wieder Quadrate (Zweige) an, an deren gegenüberliegenden Seiten sich wiederum rechtwinklige Dreiecke befinden, die dem ersten Dreieck ähnlich sind usw. Alle entstehenden Verzweigungen enden mit Quadraten (Blättern). Für welche rechtwinkligen Dreiecke ist es möglich, jeden Pythagorasbaum durch Hinzufügen von weiteren Dreiecken und Quadraten so wachsen zu lassen, dass er höchstens zwei verschiedene Größen von Blättern besitzt?

Setzen wir ein rechtwinklig gleichschenkliges Dreieck auf das Ausgangsquadrat und fügen an die Katheten zwei Quadrate an, auf deren gegenüberliegenden Seiten wieder rechtwinklige Dreiecke sitzen usw., erhalten wir einen symmetrischen Pythagorasbaum (Abbildung oben links). Er besitzt nur eine Größe von Blättern. Nach dem Pythagorassatz sind die jeweiligen Kathetenquadrate in ihrer Kantenlänge immer um einen Faktor √2 kleiner als das Hypotenusenquadrat. Wenn man den Baum nicht an allen Stellen in gleicher Weise entwickelt, wird er unsymmetrisch und hat mehrere Größen von Blättern (Abbildung oben rechts). Es leuchtet unmittelbar ein, dass wir jeden solchen Baum, wenn wir alle größeren Blätter in Zweige verwandeln, so weiterentwickeln können, dass er nur noch eine Größe von Blättern besitzt. Damit haben wir die einzige Lösung für nur eine Blattgröße, weil ein ungleichschenkliges Dreieck notwendigerweise zu mindestens zwei Blattgrößen führen würde.

Auf einfache Weise können wir jeden solchen Baum so verwandeln, dass er genau zwei Blattgrößen besitzt. Dazu brauchen wir nur auf einige Blätter Dreiecke zu setzen und darauf zwei kleinere, aber untereinander gleiche Quadrate als neue Blätter. Die Abbildung oben rechts kann wieder als Beispiel dienen. Wir haben also auch hier eine einfache Lösung gefunden. Gibt es außer dem gleichschenkligen Dreieck noch weitere Lösungen für zwei Blattgrößen?

Betrachten wir dazu die drei Fälle, wie die vorletzten Verzweigungen eines Baumes fortgesetzt werden können (gelbe Dreiecke in der Abbildung unten links). Fall 1 scheidet als Lösung aus, weil beispielsweise das linke der vier Blätter kleiner sein muss als die beiden rechten Blätter und damit mindestens drei Blattgrößen vorhanden wären. Genauso muss im Fall 2 das rechte Blatt größer sein als die beiden linken. Nur im Fall 3 können wir erreichen, dass die beiden äußeren Blätter gleich groß sind und es dann nur zwei Blattgrößen gibt. Zur Herleitung der dafür notwendigen Bedingung wird die Länge der Hypotenuse des gelben Dreiecks gleich 1 und die seiner längeren Kathete gleich x gesetzt. Damit hat auch die Hypotenuse des roten Dreiecks die Länge x. Für die längere Kathete x' des roten Dreiecks gilt aufgrund der Ähnlichkeit des gelben und des roten Dreiecks:

x' / x = x / 1

x ' = x²

Die längere Kathete x' des roten Dreiecks hat also die Länge x². Damit nun zwei gleich große Blätter entstehen, muss die kürzere Kathete des gelben Dreiecks genau so lang sein wie die längere Kathete des roten Dreiecks. Sie muss also ebenfalls die Länge x² haben. Das gelbe Dreieck hat somit Katheten der Länge x bzw. x² sowie eine Hypotenuse der Länge 1. Damit gilt für das gelbe Dreieck nach dem Satz des Pythagoras:

(x²)² + x² = 1

x⁴ + x² = 1

oder (mit u = x²):

u² + u - 1 = 0

u = -1/2 + 1/2·√5 = 0,618... = 1 : 1,618... (Verhältnis des goldenen Schnitts)

x = √u = 0,786...

Als einzige Lösung kommt also nur ein Dreieck in Frage, bei dem das Verhältnis von Hypotenuse zur kürzeren Kathete dem goldenen Schnitt und das Verhältnis zur längeren Kathete der Wurzel aus dem goldenen Schnitt entspricht.

Aber erfüllt dieses Dreieck wirklich die oben gestellte Bedingung, die sich ja auf den ganzen Baum bezieht? Nehmen wir an, das Ausgangsquadrat (Stamm) habe die Seitenlänge 1. Dann haben entsprechend der obigen Überlegung die beiden Kathetenquadrate nach der ersten Verzweigung die Seitenlängen x und x². Weitere Verzweigungen lassen Quadrate entstehen, deren Seitenlängen sich jeweils in gleicher Weise verkleinern und sich durch xⁿ mit n als natürlicher Zahl ausdrücken lassen. Angenommen, wir hätten einen solchen "goldenen" Baum mit vielen verschiedenen Blattgrößen, wobei die kleinsten Blätter die Seitenlängen x^k-1 und x^k haben. Wenn man nun die größeren Blätter in Zweige umwandelt und weiterentwickelt, erhält man irgendwann unweigerlich Blätter mit den beiden kleinsten Blattgrößen und hat dann einen Baum, der die Bedingung erfüllt. Das hier als Verzweigung benutzte Dreieck stellt also die einzige weitere Lösung dar. In den Abbildungen wurde die rechte Kathete als die Längere angenommen. Natürlich ist auch die gespiegelte Variante eine Lösung. Die Abbildung unten rechts zeigt ein Beispiel eines solchen "goldenen" Baumes.

So ein "goldener Baum" hat noch zwei weitere interessante Eigenschaften. Aus dem oben Gesagten geht direkt hervor, dass das Verhältnis der Seiten der beiden Kathetenquadrate gleich der Wurzel aus dem Goldenen Schnitt ist.

Das Verhältnis der Flächen der beiden Quadrate und damit das Verhältnis der beiden Blattgrößen entspricht deshalb dem Goldenen Schnitt.

Die zweite Eigenschaft bezieht sich auf die Anzahl der Blätter. Der kleinste "goldene" Baum besitzt ein größeres und ein kleineres Blatt. Im nächsten Schritt entstehen aus dem größeren Blatt zwei neue Blätter. Eins davon ist das kleinere Blatt des neuen größeren Pythagorasbaumes. Das andere Blatt und das nicht umgewandelte Blatt sind nun die beiden größeren Blätter dieses Baumes. Mathematisch gesehen ergibt sich die Anzahl der größeren Blätter eines "goldenen" Baumes aus der Summe aller Blätter des nächst kleineren "goldenen" Baumes, während die Anzahl seiner kleineren Blätter gleich der Anzahl der größeren Blätter des kleineren Baumes ist. Das entspricht aber der Definition zur Erzeugung der Fibonacci-Zahlen, von denen die ersten zwölf lauten: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 und 144. Die Anzahlen der kleineren und größeren Blätter eines "goldenen" Baumes entsprechen also zwei aufeinander folgenden Fibonacci-Zahlen.

Da das Verhältnis von zwei aufeinander folgenden Fibonacci-Zahlen sich immer mehr dem Goldenen Schnitt annähert, nähert sich auch das Verhältnis der Anzahl der Blätter für die beiden Blattgrößen bei immer größer werdenden "goldenen" Bäumen dem Goldenen Schnitt.

Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, dass ein unsymmetrischer Pythagorasbaum immer mehr als zwei unterschiedliche Blattgrößen hervorbringen müsse, da neben den beiden unterschiedlichen Blattgrößen an den Endverzweigungen sich das Wachstum an der übrigen Verzweigungen auf beiden Seiten unterschiedlich entwickelt.


Copyright © Werner Brefeld (2005; Originalrätsel)