 |
Der Tangens der drei Innenwinkel im Dreieck
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite: |
18. In einem Dreieck sei der Tangens der drei Inneninkel jeweils eine positive ganze Zahl. Wie lautet die einzige Lösung?
Wenn es überhaupt eine Lösung gibt, muss der Tangens des kleinsten Winkels gleich eins sein und der Winkel selber 45°.
Wäre der Tangens nämlich 2, würde die Winkelsumme im Dreieck mehr als 180° betragen, weil arctan(2) = 63,435° ist. Einen weiteren Winkel mit 45°
kann es nicht geben, weil für den übrig bleibenden Winkel von 90° der Tangens unendlich wäre. Der Tangens des zweitkleinsten Winkels kann aber
auch nicht 3 oder mehr betragen, da der Winkel dann größer oder gleich 71,565° wäre und damit mehr als die Hälfte des übriggebliebenen Winkels
von 135° betragen würde. Es kommt für den Tangens des zweitkleinsten Winkels also nur der Wert 2 in Frage. Diese einzige Möglichkeit ist tatsächlich
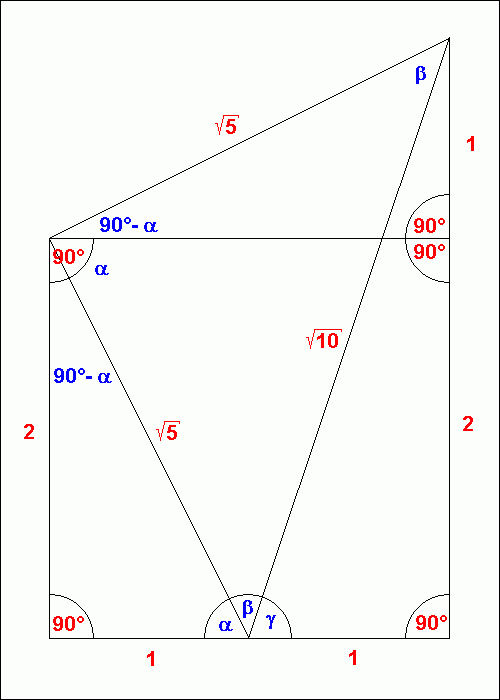
eine Lösung, wie man der Zeichnung entnehmen kann. Die Konstruktion ist so gewählt, dass α + β + γ = 180° und tan(α) = 2 ist.
Da das linke und obere Dreieck ähnlich sind, erkennt man leicht, dass tan(γ) = 3 ist. Außerdem sieht man, dass das Dreieck, dessen Ecken oben links,
oben rechts und unten in der Mitte liegen, ein rechtwinklig-gleichschenkliges Dreieck ist. β ist also gleich 45° und tan(β) = 2.
Damit ist gezeigt, dass gilt:
arc tan(1) + arc tan(2) + arc tan(3) = 180°
Die Werte für die drei Innenwinkel betragen:
Kleinster Winkel:
β = 45,000°; tan(β) = 1
Mittlerer Winkel:
α = 63,435°; tan(α) = 2
Größter Winkel:
γ = 71,565°; tan(γ) = 3
Was ist verblüffend an diesem Mathematik-Rätsel? Viele glauben intuitiv, dass es dafür keine Lösung gebe. Selbst wenn man zwei Winkel so wählt,
dass der Tangens ganzzahlig wird, so halten es viele für ausgeschlossen, dass der Tangens des dann nicht mehr frei wählbaren dritten Winkels
auch noch ganzzahlig ist, weil der Tangens eines Winkels praktisch nie eine ganze Zahl ergibt.
Links zum Thema:
Jürgen Köller: Tangensfunktion
Copyright © Werner Brefeld (2005)