 |
Teilbarkeit hochzusammengesetzter Zahlen
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
Welche Zahlen haben eine hohe Teilbarkeit, eignen sich also am besten, um etwas zu unterteilen?
Warum haben Tag und Nacht jeweils 12 Stunden, eine Stunde 60 Minuten, eine Minute 60 Sekunden und der Vollkreis 360°?
Was ist das Besondere an den oben erwähnten Zahlen 12, 60 und 360? Ziemlich schnell fällt auf, dass es sich um Zahlen mit vielen
Teilern handelt. Sie können relativ zu ihrer Größe durch ziemlich viele Zahlen ohne Rest geteilt werden und haben deshalb eine
hohe Teilbarkeit. Beispielsweise kann man die 60 durch 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 und 60 teilen, ohne dass ein Rest bleibt.
Im Gegensatz dazu kann man Primzahlen wie z.B. die 7 nur durch 1 und durch sich selbst teilen. Zahlen mit mehr als 2 Teilern sind
deshalb keine Primzahlen, sondern sind aus Primfaktoren zusammengesetzt. Deshalb heißen sie zusammengesetzte Zahlen. Wenn man von diesen
Zahlen diejenigen mit vielen Teilern sucht, dann findet man darunter auch die sogenannten hochzusammengesetzten Zahlen.
Diese Zahlen zeichnen sich dadurch aus, dass sie mehr Teiler besitzen als jede kleinere Zahl.
Die Zahl 24 mit ihren 8 Teilern 1, 2, 3, 4, 6, 8, 12 und 24 ist
eine solche hochzusammengesetzte Zahl, weil keine Zahl unter 24 so viele Teiler besitzt. Obwohl die 1 und die 2 nicht zusammengesetzt
sind, werden sie meistens zu den hochzusammengesetzten Zahlen gerechnet, weil sie ebenfalls mehr Teiler besitzen als jede kleinere Zahl.
Es gibt unendlich viele hochzusammengesetzte Zahlen. Die kleinsten sind:
1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, ...
Um die Teilbarkeit dieser Zahlen zu veranschaulichen, sind in der folgenden Zusammenstellung hinter den hochzusammengesetzten
Zahlen ihre Teilerzahlen in Klammern hinzugefügt:
1 (1), 2 (2), 4 (3), 6 (4), 12 (6), 24 (8), 36 (9), 48 (10), 60 (12), 120 (16), 180 (18), 240 (20), 360 (24),
720 (30), 840 (32), 1260 (36), 1680 (40), 2520 (48), 5040 (60), 7560 (64), 10080 (72), ...
Man erkennt, dass auch die oben erwähnten Zahlen 12, 60 und 360 zu den hochzusammengesetzten Zahlen gehören.
Aber sie zeichnet noch die weitere Eigenschaft aus, dass sie in besonderer Weise hochzusammengesetzt sind.
Besonders hochzusammengesetzt ist eine Zahl dann, wenn sie nicht nur mehr Teiler besitzt als jede kleinere Zahl,
sondern wenn sie erst von ihrer doppelt so großen Zahl in der Anzahl der Teiler übertroffen wird. So wird die 12
erst von der 24 und die 60 erst von der 120 in der Anzahl der Teiler geschlagen. Das ist deshalb eine
besondere Eigenschaft, weil die Verdoppelung einer Zahl immer zu einer Vergrößerung der Teilerzahl führt.
Jede Zahl Z lässt sich nämlich als Produkt ihrer Primfaktoren ausdrücken:
Z = 2a · 3b · 5c · 7d · ...
Dabei sind a, b, c und d natürliche Zahlen. Die Teilerzahl T der Zahl Z bekommt man, indem man alle möglichen
Kombinationen der Primfaktoren dieser Zahl bildet. Kommt die Primzahl 2 also a-mal vor, dann kann die 2 in den
verschiedenen Teilern von Z entweder a-mal, (a-1)mal, ..., zweimal, einmal oder keinmal vorkommen. Es gibt also
(a + 1) Möglichkeiten. Unabhängig davon gibt es für die Primzahl 3 dann (b + 1) Möglichkeiten.
Die Teilerzahl T beträgt also: T = (a + 1) · (b + 1) · (c + 1) · (d + 1) · ...
Die Zahl 24 lässt sich beispielsweise als 23 · 31 darstellen.
Also ist hier a = 3 und b = 1. Damit ist die Teilerzahl von 24 gleich (3 + 1) · (1 + 1) = 8.
Verdoppelt man nun eine Zahl Z, dann kommt ein Primfaktor 2 dazu, a erhöht sich damit um 1 und T wird deshalb größer.
Es gibt insgesamt nur 7 Zahlen, die auch die oben erwähnte besondere Bedingung erfüllen (siehe Beweis unten):
1, 2, 6, 12, 60, 360, 2520
Beispielsweise wird die 60, die 12 Teiler besitzt, erst von der 120 mit ihren 16 Teiler überholt, während die 24 (8 Teiler)
schon von der 36 mit ihren 9 Teilern geschlagen wird.
Der Vorteil der guten Teilbarkeit der 12 (Dutzend), der 60 (Schock) und der 360 (Anzahl der Grade des Vollkreises)
leuchten ja unmittelbar ein. Auch die 6 ist sehr gebräuchlich. Die meisten Getränkekästen haben ja 6 oder 12 Flaschen.
Die 1 als Startzahl und die 2 als kleinste Primzahl sind, wie schon erwähnt, nicht wirklich zusammengesetzt, und die
2520 ist wohl zu groß, um für die Praxis von Nutzen zu sein.
Die guten babylonischen Mathematiker könnten durchaus die besonders gute Teilbarkeit dieser Zahlen gekannt haben.
In Babylonien wurde um 1800 v. Chr. von den Sumerern das Sexagesimalsystem (60er-System) übernommen, dessen Anfänge
bis 3000 v. Chr. zurückreichen. Der Tag hatte in Babylonien 12 Doppelstunden und es gab 12 Tierkreiszeichen entlang
der scheinbaren Bahn der Sonne am Himmel. Der Vollkreis wurde in 360° eingeteilt, obwohl die Babylonier wussten,
dass das Jahr etwas mehr als 365 Tage hatte. Das Sexagesimalsystem diente dann als Vorbild beim Einteilen der Stunde
in 60 Minuten und der Minute in 60 Sekunden.
Eingehend erforscht wurden die Eigenschaften der hochzusammengesetzten Zahlen und speziell ihre Teilbarkeit erst
von einem der berühmtesten Mathematiker des 20. Jahrhunderts, dem Inder Srinivasa Ramanujan.
Der folgende Beweis durch Ausschluss zeigt, dass es nur 7 besonders hochzusammengesetzte Zahlen gibt,
also hochzusammengesetzte Zahlen, die erst von ihrem Doppelten in der Zahl ihrer Teiler übertroffen werden:
Welche hochzusammengesetzten Zahlen werden schon vorher in der Zahl ihrer Teiler übertroffen?
Hochzusammengesetzte Zahlen Z kann man nach Ramanujan darstellen als:
Z = 2x · 3y · 5z ... mit x >= y, y >= z, ...
Wandelt man Z in
Z1 = 2x–1 · 3y+1 · 5z ... ( Z1 / Z = 3 / 2 ) oder in
Z2 = 2x+2 · 3y–1 · 5z ... ( Z2 / Z = 4 / 3 ) um,
erhält man Zahlen, die kleiner als das Doppelte von Z sind. Damit die Zahl ihrer Teiler größer als die von Z ist, muss gelten:
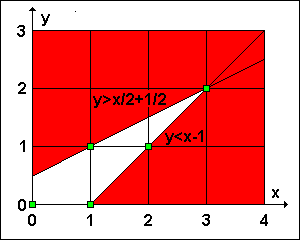
x · (y + 2) > (x + 1) · (y + 1); xy + 2x > xy + x + y + 1; x > y + 1; y < x – 1
beziehungsweise
(x + 3) · y > (x + 1) · (y + 1); xy + 3y > xy + x + y + 1; 2y > x + 1; y > ½·x + ½
Für alle Werte von x und y, die diesen Ungleichungen genügen, lassen sich also Zahlen konstruieren,
die mehr Teiler als Z haben, aber nicht doppelt so groß wie Z sind.
Nur die folgenden 5 Wertepaare für x und y werden von den Ungleichungen nicht abgedeckt
und müssen deshalb einzeln untersucht werden:
x = 0 und y = 0:
Z = 20 = 1 (wird erst von ihrem Doppelten in ihrer Teilerzahl übertroffen)
x = 1 und y = 0:
Z = 21 = 2 (wird erst von ihrem Doppelten in ihrer Teilerzahl übertroffen)
x = 1 und y = 1:
Z = 21 · 31 = 6 (wird erst von ihrem Doppelten in ihrer Teilerzahl übertroffen)
Z = 21 · 31 · 51 · r (kann in Z1 = 22 · 32 · r umgewandelt werden;
Z1/Z = 6/5 < 2; Teiler(Z1) / Teiler(Z) = 9/8 > 1)
x = 2 und y = 1:
Z = 22 · 31 = 12 (wird erst von ihrem Doppelten in ihrer Teilerzahl übertroffen)
Z = 22 · 31 · 51 = 60 (wird erst von ihrem Doppelten in ihrer
Teilerzahl übertroffen)
Z = 22 · 31 · 51 · 71 · r
(kann in Z1 = 24 · 32 · 51 · r umgewandelt werden;
Z1/Z = 12/7 < 2; Teiler(Z1) / Teiler(Z) = 30/24 > 1)
x = 3 und y = 2:
Z = 23 · 32 = 72 (wird schon von 23 · 31 · 51 = 120 in
ihrer Teilerzahl übertroffen; 16 Teiler statt 12 Teiler)
Z = 23 · 32 · 5 = 360 (wird erst von ihrem Doppelten in ihrer
Teilerzahl übertroffen)
Z = 23 · 32 · 51 · 71 = 2520 (wird erst von ihrem
Doppelten in ihrer Teilerzahl übertroffen)
Z = 23 · 32 · 51 · 71 · 111 · r
(kann in Z1 = 24 · 34 · 51 · 71 · r
umgewandelt werden; Z1/Z = 18/11 < 2; Teiler(Z1) / Teiler(Z) = 100/96 > 1)
Z = 23 · 32 · 52 · r (kann in Z1 = 24 · 33 · 51 · r
umgewandelt werden; Z1/Z = 6/5 < 2; Teiler(Z1) / Teiler(Z) = 40/36 > 1)
Ergebnis: Bis auf die sieben Zahlen 1, 2, 6, 12, 60, 360 und 2520 werden alle hochzusammengesetzten
Zahlen Z schon von Zahlen in ihrer Teilerzahl übertroffen, die kleiner als das Doppelte von Z sind.
Links zum Thema:
Achim Flammenkamp: Highly Composite Numbers
On-Line Encyclopedia of Integer Sequences:
Special Highly Composite Numbers
Horst Gierhardt: Der berühmte Mathematiker Srinivasa Ramanujan
Copyright © Werner Brefeld (1999; Originalquelle)

