 |
Regelmäßige Vielecke und Einheitskreis
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite: |
25. Einem Einheitskreis werden beliebige regelmäßige Vielecke einbeschrieben und umbeschrieben. Welche dieser Vielecke haben einen ganzzahligen Flächeninhalt?
Eine sehr einfache Lösung dieser Aufgabe stellt das dem Einheitskreis umbeschriebene Quadrat dar. Da der Einheitskreis
den Radius 1 besitzt, ist die Seitenlänge dieses Quadrats 2. Die Fläche des Quadrats ist demnach gleich 4 und damit
ganzzahlig. Auch das Auffinden einer zweiten Lösung ist nicht besonders schwer. Wie man leicht erkennt, ist die
Diagonale eines einbeschriebenen Quadrats gleich 2. Nach dem Satz des Pythagoras ergibt sich dadurch für die Länge
einer Seite der Wert √2. Die Fläche ist also hier 2 und damit wiederum ganzzahlig.
Gibt es jedoch noch weitere Lösungen?
Betrachtet man zunächst die umbeschriebenen regelmäßigen Vielecke, so sieht man, dass sich jedes dieser n-Ecke
in n gleichschenklige und gleich große Dreiecke zerlegen lässt. Alle diese Dreiecke haben die Höhe 1. Die
Winkel an der Spitze des Dreiecks haben den Wert 360°/n. Für die Länge der halben Grundseite ergibt sich dann
der Wert tan(360°/2n) oder tan(180°/n). Die Fläche der gleichschenkligen Dreiecke ist ebenfalls tan(180°/n).
Damit ergibt sich für die Fläche des umbeschriebenen n-Ecks: Fum(n) = n · tan(180°/n).
Je größer n wird, desto kleiner wird die Fläche, weil Fum(n) einerseits durch den Faktor n proportional zu n steigt,
andererseits gleichzeitig durch den Faktor tan(180°/n) mehr als proportional sinkt. Der Grund liegt in der Steigung
der Tangens-Funktion, die bis auf eine Stelle immer größer als 1 ist. Für ein Dreieck ist
Fum(3) = 3 · tan(60°) = 3 · √3 = 5,196. Für ein Quadrat ergibt sich der schon erwähnte Wert von
Fum(4) = 4 · tan(90°) = 4. Die Werte für Fum(n) können nicht bis auf 3 sinken, weil der Einheitskreis
schon die Fläche π besitzt. Für die umbeschriebenen Vielecke gibt es also keine weitere Lösung.
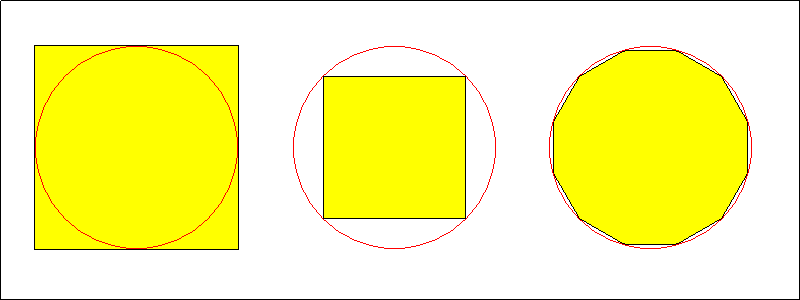
Die einbeschriebenen regelmäßigen n-Ecke kann man ebenso in n gleichschenklige und gleich große Dreiecke zerlegen.
Hier ist die Länge aller Schenkel gleich 1. Die Länge der Höhe ist dann cos(360°/2n) und die Länge der
halben Grundseite sin(360°/2n). Die Fläche eines gleichschenkligen Dreiecks beträgt folglich
sin(360°/2n) · cos(360°/2n).
Und schließlich ist die Fläche des einbeschriebenen n-Ecks:
Fein(n) = n · sin(360°/2n) · cos(360°/2n) = n/2 · sin(360°/n)
(Ausnutzung des Additionstheorems für den Sinus: sin(2α) = 2 · sin(α) · cos(α))
Je größer n wird, desto größer wird hier die Fläche, weil Fein(n) einerseits durch den Faktor n/2 proportional zu n steigt,
andererseits gleichzeitig durch den Faktor sin(360°/n) weniger als proportional sinkt. Die Steigung der Sinus-Funktion
ist nämlich bis auf eine Stelle immer kleiner als 1. Ein einbeschriebenes Dreieck hat demnach die Fläche
Fein(3) = 3/2 · sin(120°) = 3/2 · 1/2 · √3 = 3/4 · √3 = 1,299. Beim Quadrat ergibt sich der schon
genannte Wert von 2. Da der Einheitskreis ja die Fläche π besitzt, kann es für die einbeschriebenen Vielecke höchstens
noch eine Lösung geben und die Fläche müsste gleich 3 sein.
Das kleinste Wert von n, der größer als 4 ist und bei dem der sin(360°/n) rational ist, beträgt 12.
Die Fläche des einbeschriebenen Zwölfecks ist entsprechend Fein(12) = 12/2 · sin(360°/n) = 6 · sin(30°) = 6 · 1/2 = 3.
Das Zwölfeck hat tatsächlich eine Fläche mit dem gesuchten Wert von 3 und ist demnach die dritte und
letzte der gesuchten Lösungen.
Was ist verblüffend an diesem Mathematik-Rätsel? Viele glauben intuitiv, dass es neben den beiden leicht
zu findenden Lösungen keine weitere Lösung gebe.
Überträgt man die Frage dieses Mathematik-Rätsels auf den dreidimensionalen Raum, dann geht es um die Einheitskugel
und die Platonischen Körper Tetraeder, Hexaeder (Würfel), Oktaeder, Dodekaeder und Ikosaeder. Wenn man diese fünf
Polyeder einer Einheitskugel einbeschreibt und umbeschreibt, gibt es dann einen unter ihnen, der ein ganzzahliges
Volumen hat? Leider gibt es für dieses Problem keine verblüffende Lösung. Der einzige Platonische Körper, der die
obige Bedingung erfüllt, ist der umbeschriebene Würfel. Da die Einheitskugel den Radius 1 besitzt, ist die Seitenlänge
dieses Würfels gleich 2. Das Volumen des Würfels ist demnach gleich 8 und damit ganzzahlig.
Hier folgt eine Zusammenstellung von Formeln für die Flächeninhalte einiger ausgewählter regelmäßiger Vielecke mit der Seitenlänge s:
Dreieck: F = 0,433013 s2 = 1/4 · √3 · s2
Quadrat: F = 1,000000 s2 = s2
Fünfeck: F = 1,720477 s2 = 1/4 · √(25 + 10·√5) ·s2
Sechseck: F = 2,598076 s2 = 3/2 · √3 · s2
Achteck: F = 4,828427 s2 = 2 · (1 + √2) · s2
Zehneck: F = 7,694209 s2 = 5/2 · √(5 + 2·√5) · s2
Zwölfeck: F = 11,196152 s2 = 3 · (2 + √3) · s2
Copyright © Werner Brefeld (2006)