 |
Regelmäßiges Vieleck und Zerschneiden (Sechseck und Zwölfeck)
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite: |
2. Welche Möglichkeiten gibt es, ein beliebiges regelmäßiges Vieleck in mehrere regelmäßige Vielecke mit der gleichen Seitenlänge zu zerschneiden?
An jeder Ecke des gesuchten großen regelmäßigen Vielecks können nur genau zwei kleinere
regelmäßige Vielecke zusammenstoßen, wobei die Summe ihrer Innenwinkel kleiner als 180° sein muss. Für drei
oder mehr regelmäßige Vielecke an jeder Ecke gibt es keine Lösung, weil das kleinste regelmäßige Vieleck,
nämlich das Dreieck, schon einen Innenwinkel von 60° besitzt. Die Winkelsumme betrüge also mindestens 180°.
Mit diesen Randbedingungen gibt es nur drei Möglichkeiten:
1. Zwei kleine Dreiecke (Winkelsumme: 120°)
2. Ein kleines Dreieck und ein kleines Quadrat (Winkelsumme: 150°)
3. Ein kleines Dreieck und ein kleines Fünfeck (Winkelsumme: 168°)
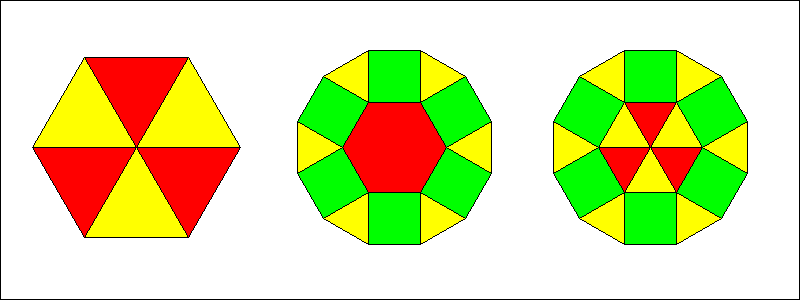
Die erste Möglichkeit ergibt sofort als Lösung ein großes regelmäßiges Sechseck, dass man in 6 kleine
regelmäßige Dreiecke zerschneiden kann.
Bei der zweiten Möglichkeit entsteht ein großes regelmäßiges Zwölfeck, bei dem sich in der Mitte noch ein
kleines regelmäßiges Sechseck mit den richtigen Bedingungen befindet. Aus dieser zweiten Lösung kann man
unter Verwendung der ersten Lösung eine dritte Lösung gewinnen, indem man das Sechseck in Dreiecke zerlegt
(siehe Abbildung).
Die dritte Möglichkeit führt auf ein regelmäßiges 30-Eck mit Dreiecken und Fünfecken an den Rändern.
Allerdings entsteht in der Mitte ein Stern mit 15 Zacken und Innenwinkeln von jeweils 84°. Daraus kann
man durch Zerschneiden keine regelmäßigen Vielecke mit den geforderten Eigenschaften mehr herstellen.
Es bleibt also bei den folgenden drei Lösungen:
1. Zerschneiden eines regelmäßigen Sechsecks in 6 regelmäßige Dreiecke
2. Zerschneiden eines regelmäßigen Zwölfecks in 6 regelmäßige Dreiecke, 6 Quadrate und 1 regelmäßiges Sechseck
3. Zerschneiden eines regelmäßiges Zwölfecks in 12 regelmäßige Dreiecke und 6 Quadrate
Was ist verblüffend an diesem Mathematik-Rätsel? Viele glauben intuitiv, dass es neben der meistens bekannten
Zerlegung eines regelmäßigen Sechsecks in sechs regelmäßige Dreiecke keine weiteren Lösungen gebe.
Referenz: Mathematik-Olympiade, Aufgabe 430813
Links zum Thema:
Jürgen Köller: Regelmäßiges Vieleck
Jürgen Köller: Regelmäßiges Zwölfeck
Copyright © Werner Brefeld (2000)