 |
Fußball, Platonische Körper und Archimedische Körper
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
Welcher platonische Körper oder archimedische Körper eignet sich am besten als Fußball?
Warum besteht der Fußball oft aus 20 regelmäßigen Sechsecken und 12 regelmäßigen Fünfecken?
Meistens wird ein Fußball aus Lederstücken zusammengenäht, die die Form von regelmäßigen Vielecken besitzen.
Dabei wählt man eine regelmäßige Anordnung der Vielecke. Das bedeutet, dass jede Ecke, an der die Vielecke zusammenstoßen,
gleich aussieht. Körper mit nur einer Sorte von regelmäßigen Vielecken auf ihrer Oberfläche nennt man platonische Körper, Körper
mit mehr Sorten archimedische Körper. Bei jedem Körper liegen die Eckpunkte auf einer Kugeloberfläche. Sie besitzen also
eine Umkugel. Das macht sie als Kandidaten für die Herstellung eines Fußballs sehr attraktiv.
Es gibt 5 platonische Körper und 13 archimedische Körper, wenn man die Prismen und Antiprismen nicht mitzählt. Unter diesen
18 Körpern wählt man nun die aus, die möglichst rund sind, bei denen das Verhältnis von Inkugelradius zu Umkugelradius also
möglichst groß ist. Während sowohl platonische Körper als auch archimedische Körper Umkugeln besitzen, haben streng genommen
nur platonische Körper Inkugeln. Bei den archimedischen Körpern besitzt jede Sorte von regelmäßigen Vielecken eine andere
Inkugel. Alle diese Inkugeln haben aber den gleichen Mittelpunkt. Die Inkugel mit dem jeweils kleinsten Inkugelradius wurde bei den
Berechnungen zugrunde gelegt. Die nach der obigen Definition rundesten vier Körper sind ausschließlich archimedische Körper:
| Körper | Inkugelradius/ | Anzahl der | Anzahl der | Anzahl der |
| | Umkugelradius | Flächen | Flächen | Kanten |
| | | pro Ecke | | |
| | | | | |
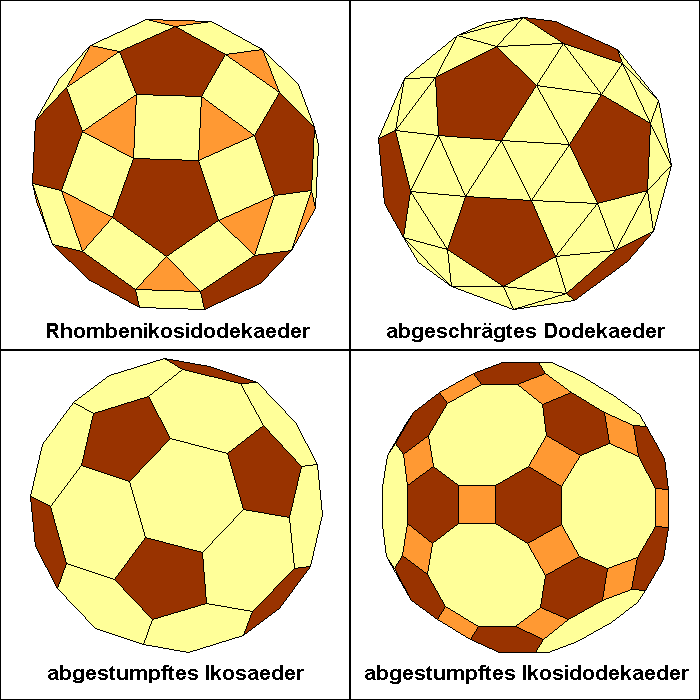
| Rhombenikosidodekaeder | 92,46% | 4 | 62 | 120 |
| abgeschrägtes Dodekaeder | 91,89% | 5 | 92 | 150 |
| abgestumpftes Ikosaeder | 91,50% | 3 | 32 | 90 |
| abgestumpftes Ikosidodekaeder | 90,49% | 3 | 62 | 180 |
Auch die unendlich vielen Prismen und Antiprismen sind nicht annähernd so rund wie diese vier archimedischen
Körper. Außerdem werden die Prismen und Antiprismen mit steigender Eckenzahl der beiden sich gegenüberliegenden Vielecke immer dünner
und dadurch das Verhältnis von Inkugelradius zu Umkugelradius immer kleiner.
Es ist nachteilig, viele Flächen an einer Ecke zusammennähen zu müssen. Daher wird man unter den rundesten Körper diejenigen
bevorzugen, bei denen nur drei Flächen an einer Seite zusammentreffen. Außerdem ist es vorteilhaft, wenn der Körper
nicht zu viele Flächen und Kanten besitzt. Durch die Zahl der Kanten wird ja die Zahl der benötigten Nähte bestimmt.
Unter Berücksichtigung dieser Randbedingungen fällt die Wahl auf das abgestumpfte Ikosaeder mit seinen 12 regelmäßigen Fünfecken
und 20 regelmäßigen Sechsecken.
Ein weiterer Aspekt ist, dass die durch die unterschiedlichen regelmäßigen Vielecke hervorgerufenen Unterschiede
in den Abweichungen von der Kugelform möglichst klein ausfallen sollen. Das ist dann der Fall, wenn sich die
regelmäßigen Vielecke auf der Oberfläche in ihrer Größe möglichst wenig unterscheiden. Auch hier schneidet das
abgestumpfte Ikosaeder mit seinen Fünfecken und Sechsecken unter den rundesten archimedischen Körpern am besten
ab.
Tatsächlich haben auch fast alle Fußbälle die Grundform eines abgestumpften Ikosaeders. Selten kann man auch einen
Fußball in Form eines Rhombenikosidodekaeders mit seinen 20 regelmäßigen Dreiecken, 30 Quadraten und 12
regelmäßigen Fünfecken antreffen. Die Web-Seite über Platonische Körper und Archimedische Körper
enthält weitere Informationen über diese interessanten Polyeder.
Man kann ein abgestumpftes Ikosaeder nach der oben angegebenen Definition noch runder machen kann, wenn man die Fünfecke
weiter vergrößert, indem man das Ikosaeder weiter abstumpft. Das ist möglich, weil die kleinste Inkugel
nur die Sechsecke berührt. Eine weitere Abstumpfung führt dann dazu, dass sich die Fünfecke dieser Inkugel annähern. Bis zur Berührung
der Inkugel durch die Fünfecke ändert sich also der kleinste Inkugelradius nicht, während der Umkugelradius abnimmt. Der Körper wird also
runder. Allerdings verändert sich dann das regelmäßige Sechseck zu einem Sechseck, das abwechselnd verlängerte und verkürzte Seiten besitzt.
Die verlängerten Seiten sind natürlich genauso lang wie die Fünfeckseiten, an denen sie angrenzen. Eine entsprechende Rechnung
ergibt, dass dann die verkürzten Sechseckseiten 69,198% der Länge der Fünfeckseiten haben.
Für den so entstandenen optimierten Fußball vergrößert sich das Verhältnis von kleinstem Inkugelradius zu Umkugelradius
von 91,50% auf 92,26%. Damit ist dieser Körper sogar noch runder als das abgeschrägte Dodekaeder mit 91,94%
und fast so rund wie das Rhombenikosidodekaeder mit 92,46%.
Gelegentlich wird auch der sogenannte "Große Fußball" (siehe Abbildung) als Möglichkeit genannt, einen Fußball
herzustellen. Dieser Körper besitzt 12 Fünfecke und 30 Sechsecke, also insgesamt 42 Flächen. Die Anzahl der Kanten
beträgt 120. Man erhält so ein Polyeder, wenn man die Kanten eines Dodekaeders geeignet abschneidet.
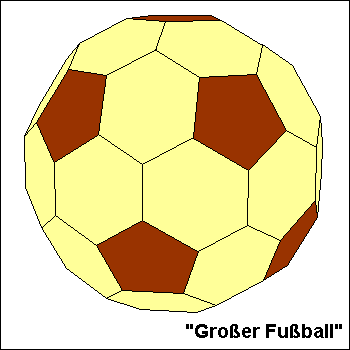
Allerdings ist dieses Polyeder kein archimedischer Körper, weil seine 30 Sechsecke nicht regelmäßig sind. Wären sie regelmäßig,
müssten jeweils drei Sechsecke, die an einer Ecke zusammenstoßen, eine ebene Fläche bilden, weil die Winkelsumme ihrer Innenwinkel 360° betrüge.
Man erkennt, dass dann sogar alle Sechsecke des "Großen Fußballs" auf einer Ebene liegen müssten. Tatsächlich sind jedoch die Innenwinkel an
der Stelle, wo drei Sechsecke zusammenkommen, nicht 360°/3 = 120°, sondern 2 · arctan(½ + ½·√5) = 116,565°.
Die vier übrigen Innenwinkel sind gleich und betragen 121,7175°. Im Gegensatz zu einem archimedischen Körper besitzt der "Große Fußball"
keine eindeutig definierte Umkugel.
Links zum Thema:
Wikipedia: Archimedischer Körper - Wikipedia
Jürgen Köller: Abgestumpftes Ikosaeder
Arndt Brünner: Platonische Körper und Archimedische Körper
Copyright © Werner Brefeld (2005; Originalquelle)


