 |
Platonische Körper und Archimedische Körper (reguläre und halbreguläre Polyeder)
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
Während platonische Körper an ihrer Oberfläche nur regelmäßige Vielecke einer Sorte besitzen,
haben archimedische Körper regelmäßige Vielecke von mehr als einer Sorte.
Die Ecken dieser Körper sehen jeweils alle gleich aus. An jeder Ecke stoßen also die gleichen regelmäßigen Vielecke
in gleicher Anzahl und gleicher Anordnung zusammen. Von jeder Ecke aus betrachtet haben alle Flächen die gleiche
Anordnung. Alle diese Körper liegen auf der Oberfläche einer umhüllenden Umkugel. Es gibt genau
5 platonische Körper und 13 archimedische Körper, wobei erwähnt werden sollte, dass zwei archimedische Körper
(abgeschrägtes Hexaeder und abgeschrägtes Dodekaeder) in jeweils zwei spiegelbildlich entgegengesetzten Varianten
auftreten. Die folgende Abbildung zeigt die 5 platonischen Körper und die 13 archimedischen Körper:
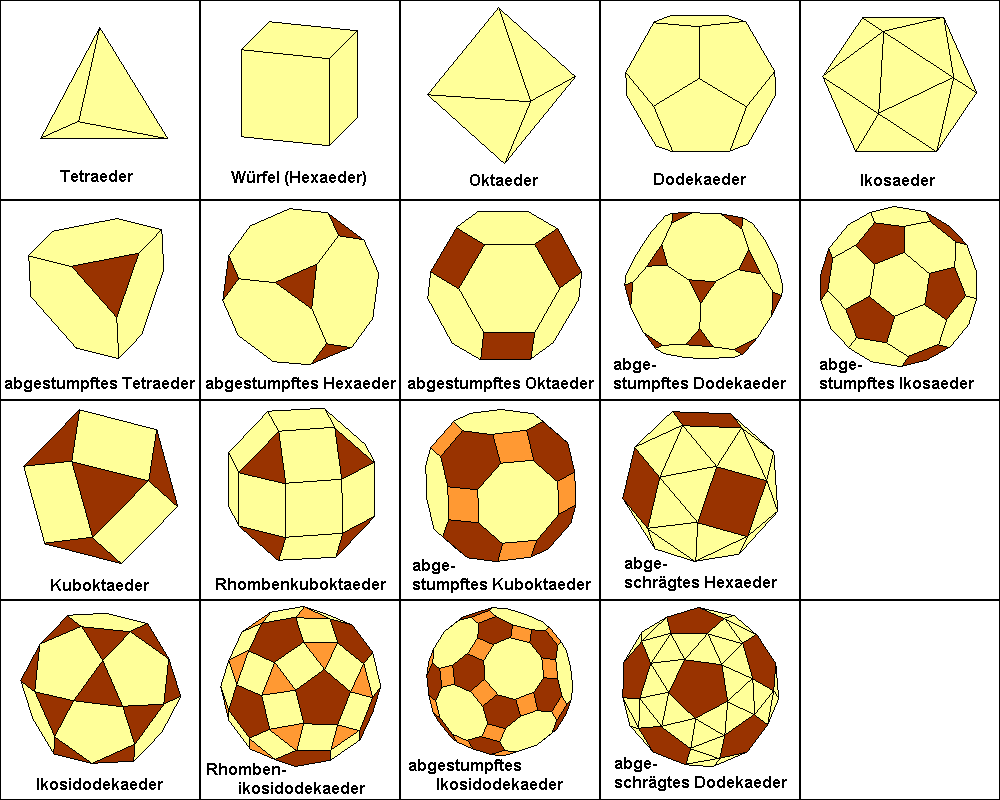
Zusätzlich gibt es noch unendlich viele Prismen und Antiprismen, die die obigen Bedingungen erfüllen. Die Prismen
und Antiprismen haben als Deckenfläche und Bodenfläche jeweils ein regelmäßiges Vieleck. Die Seitenflächen bestehen
beim Prisma aus Quadraten und beim Antiprisma aus gleichseitigen Dreiecken. Dass es nicht mehr Polyeder dieser Art gibt,
kann man durch Betrachtung der Anordnung und der Innenwinkel der an jeder Ecke zusammenstoßenden Vielecke zeigen.
Es müssen ja an jeder Ecke mindestens 3 Vielecke zusammenstoßen und die Summe ihrer zusammenstoßenden Innenwinkel
muss kleiner als 360° sein. Daraus folgt, dass es nicht mehr als 5 platonische Körper geben kann, weil man nur
3, 4 oder 5 gleichseitige Dreiecke, 3 Quadrate oder 3 regelmäßige Fünfecke unter den angegebenen Bedingungen
zusammenfügen kann.
Überträgt man diese Überlegungen auf den zweidimensionalen Raum, so muss man Vielecke suchen, die einen
Umkreis besitzen. Besteht der Rand ("Oberfläche") dieser Vielecke aus gleich langen Strecken, bekommt man
regelmäßige Vielecke, die den platonischen Körpern im dreidimensionalen Raum entsprechen. Davon gibt es
unendlich viele. Sind die begrenzenden Strecken verschieden lang, könnte man von "archimedischen Körpern"
sprechen, deren Anzahl ebenfalls unendlich wäre.
Vierdimensionale "Polyeder" werden Polytope genannt. Sie haben dreidimensionale "Oberflächen", die Facetten heißen.
Im vierdimensionalen Raum entsprechen den 5 platonischen und 13 archimedischen Körpern 6 reguläre und 3 halbreguläre
Polytope. Diese Körper besitzen platonische Körper als Facetten, wobei die regulären Polytope nur eine Sorte von
platonischen Körpern haben. Es existiert ein reguläres Polytop mit 5 Tetraedern als Facetten. Es wird Simplex genannt
und entspricht dem Tetraeder im dreidimensionalen Raum. Ein weiterer Körper mit 8 Würfeln als Facetten heißt Tesserakt
oder Hyperwürfel. Das Kreuzpolytop hat 16 Tetraeder als Facetten und ist mit dem Oktaeder verwandt. Dem Dodekaeder und
Ikosaeder entsprechen im vierdimensionalen Raum das 120-Zell und das 600-Zell. Diese beiden regulären Polytope werden
von 120 Dodekaedern bzw. 600 Tetraedern begrenzt. Schließlich gibt es noch das 24-Zell mit 24 Oktaedern als Facetten.
Für dieses Polytop gibt es keine Entsprechung unter den platonischen Körpern. Die 3 halbregulären Polytope haben als
Facetten 5 Tetraeder und 5 Oktaeder, 120 Tetraeder und 24 Ikosaeder, und 600 Oktaeder und 120 Ikosaeder.
An jeder Kante dieser Polytope müssen mindestens 3 platonische Körper zusammenstoßen und die Summe ihrer zusammenstoßenden
Flächenwinkel muss kleiner als 360° sein. Daraus folgt, dass es im vierdimensionalen Raum nicht mehr als 6 reguläre Polytope
geben kann, weil man nur 3, 4 oder 5 Tetraeder, 3 Würfel, 3 Oktaeder oder 3 Dodekaeder unter den angegebenen Bedingungen
zusammenfügen kann. Ab dem fünfdimensionalen Raum gibt es jeweils nur noch drei reguläre Polytope. Sie entsprechen dem
Tetraeder, dem Hexaeder (Würfel) und dem Oktaeder im dreidimensionalen Raum.
Erzeugung von platonischen und archimedischen Körpern aus platonischen Körpern
Schneidet man von einem Tetraeder die 4 Ecken so ab, dass aus den 4 gleichseitigen Dreiecken 4 regelmäßige Sechsecke werden,
erhält man ein abgestumpftes Tetraeder.
Schneidet man die Ecken noch stärker ab, dass wieder 4 gleichseitige, aber kleinere Dreiecke entstehen, erhält man ein Oktaeder.
Schneidet man die Ecken weiter ab, dass die Dreiecke sich weiter verkleinern und die Schnittflächen die Form eines regelmäßiges Sechsecks
annehmen, entsteht wieder ein abgestumpftes Tetraeder.
Schneidet man schließlich die Ecken so stark ab, dass die 4 gleichseitigen Dreiecke zu einem Punkt schrumpfen, erhält man das zum
Ausgangstetraeder duale Tetraeder.
Schneidet man dagegen von einem Tetraeder die 6 Kanten und die 4 Ecken so ab, dass neben den verkleinerten 4 gleichseitigen Dreiecken
noch 6 Quadrate und weitere 4 gleichseitige Dreiecke entstehen, erhält man ein Kuboktaeder.
Dieses Polyeder bekommt man auch, wenn man von einem Tetraeder die gleichseitigen Dreiecke so weit auseinander zieht, dass Quadrate
und gleichseitige Dreiecke in die Lücken passen.
Schneidet man von einem Würfel die 8 Ecken so ab, dass aus den 6 Quadraten 6 regelmäßige Achtecke werden, erhält man ein
abgestumpftes Hexaeder.
Schneidet man die Ecken noch stärker ab, dass wieder 6 (aber kleinere) Quadrate entstehen, erhält man ein Kuboktaeder.
Schneidet man die Ecken weiter ab, dass die Quadrate sich weiter verkleinern und die Schnittflächen die Form eines regelmäßiges Sechsecks
annehmen, entsteht ein abgestumpftes Oktaeder.
Schneidet man schließlich die Ecken so stark ab, dass die 6 Quadrate zu einem Punkt schrumpfen, erhält man das zum Würfel duale Oktaeder.
Schneidet man dagegen von einem Würfel die 12 Kanten und die 8 Ecken so ab, dass neben den verkleinerten 6 Quadraten noch 12 weitere Quadrate
und 8 gleichseitige Dreiecke entstehen, erhält man ein Rhombenkuboktaeder.
Dieses Polyeder bekommt man auch, wenn man von einem Würfel die Quadrate so weit auseinander zieht, dass Quadrate und gleichseitige Dreiecke
in die Lücken passen.
Schließlich kann man ein abgestumpftes Kuboktaeder erzeugen, indem man von einem Würfel die 8 Ecken und die 12 Kanten so abschneidet,
dass aus den 6 Quadraten regelmäßige Achtecke, an den Ecken regelmäßige Sechsecke und an den Kanten Quadrate entstehen.
Schneidet man von einem Oktaeder die 6 Ecken so ab, dass aus den 8 gleichseitigen Dreiecken 8 regelmäßige Sechsecke werden,
erhält man ein abgestumpftes Oktaeder.
Schneidet man die Ecken noch stärker ab, dass wieder 8 gleichseitige, aber kleinere Dreiecke entstehen, erhält man ein Kuboktaeder.
Schneidet man die Ecken weiter ab, dass die Dreiecke sich weiter verkleinern und die Schnittflächen die Form eines regelmäßiges Achtecks
annehmen, entsteht ein abgestumpftes Hexaeder.
Schneidet man schließlich die Ecken so stark ab, dass die 8 gleichseitigen Dreiecke zu einem Punkt schrumpfen, erhält man den zum Oktaeder
dualen Würfel.
Schneidet man dagegen von einem Oktaeder die 12 Kanten und die 6 Ecken so ab, dass neben den verkleinerten 8 gleichseitigen Dreiecken
noch 18 Quadrate entstehen, erhält man ein Rhombenkuboktaeder.
Dieses Polyeder bekommt man auch, wenn man von einem Oktaeder die gleichseitigen Dreiecke so weit auseinander zieht, dass Quadrate
in die Lücken passen.
Schließlich kann man ein abgestumpftes Kuboktaeder erzeugen, indem man von einem Oktaeder die 6 Ecken und die 12 Kanten so abschneidet,
dass aus den 8 regelmäßigen Dreiecken regelmäßige Sechsecke, an den Ecken regelmäßige Achtecke und an den Kanten Quadrate entstehen.
Schneidet man von einem Dodekaeder die 20 Ecken so ab, dass aus den 12 regelmäßigen Fünfecken 12 regelmäßige Zehnecke werden,
erhält man ein abgestumpftes Dodekaeder.
Schneidet man die Ecken noch stärker ab, dass wieder 12 regelmäßige, aber kleinere Fünfecke entstehen, erhält man ein Ikosidodekaeder.
Schneidet man die Ecken weiter ab, dass die Fünfecke sich weiter verkleinern und die Schnittflächen die Form eines regelmäßiges Sechsecks
annehmen, entsteht ein abgestumpftes Ikosaeder.
Schneidet man schließlich die Ecken so stark ab, dass die 12 regelmäßigen Fünfecke zu einem Punkt schrumpfen, erhält man das zum Dodekaeder
duale Ikosaeder.
Schneidet man dagegen von einem Dodekaeder die 30 Kanten und die 20 Ecken so ab, dass neben den verkleinerten 12 regelmäßigen Fünfecken
noch 30 Quadrate und 20 gleichseitige Dreiecke entstehen, erhält man ein Rhombenikosidodekaeder.
Dieses Polyeder bekommt man auch, wenn man von einem Dodekaeder die regelmäßigen Fünfecke so weit auseinander zieht, dass Quadrate
gleichseitige Dreiecke in die Lücken passen.
Schließlich kann man ein abgestumpftes Ikosidodekaeder erzeugen, indem man von einem Dodekaeder die 20 Ecken und die 30 Kanten so
abschneidet, dass aus den regelmäßigen Fünfecken regelmäßige Zehnecke, an den Ecken regelmäßige Sechsecke und an den Kanten Quadrate
entstehen.
Schneidet man von einem Ikosaeder die 12 Ecken so ab, dass aus den 20 gleichseitigen Dreiecken 20 regelmäßige Sechsecke werden,
erhält man ein abgestumpftes Ikosaeder (Fußballkörper).
Schneidet man die Ecken noch stärker ab, dass wieder 20 gleichseitige, aber kleinere Dreiecke entstehen, erhält man ein Ikosidodekaeder.
Schneidet man die Ecken weiter ab, dass die Dreiecke sich weiter verkleinern und die Schnittflächen die Form eines regelmäßiges Zehnecks
annehmen, entsteht ein abgestumpftes Dodekaeder.
Schneidet man schließlich die Ecken so stark ab, dass die 20 gleichseitigen Dreiecke zu einem Punkt schrumpfen, erhält man das zum Ikosaeder
duale Dodekaeder.
Schneidet man dagegen von einem Ikosaeder die 30 Kanten und die 12 Ecken so ab, dass neben den verkleinerten 20 gleichseitigen Dreiecken
noch 30 Quadrate und 12 regelmäßige Fünfecke entstehen, erhält man ein Rhombenikosidodekaeder.
Dieses Polyeder bekommt man auch, wenn man von einem Ikosaeder die gleichseitigen Dreiecke so weit auseinander zieht, dass Quadrate
und regelmäßige Fünfecke in die Lücken passen.
Schließlich kann man ein abgestumpftes Ikosidodekaeder erzeugen, indem man von einem Ikosaeder die 12 Ecken und die 30 Kanten so
abschneidet, dass aus den regelmäßigen Dreiecken regelmäßige Sechsecke, an den Ecken regelmäßige Zehnecke und an den Kanten Quadrate
entstehen.
Konkretes Beispiel, wie man durch Abschneiden vom Würfel zum Oktaeder und dann wieder zum Würfel kommt:
Ausgegangen wird von einem Würfel von s = 10 cm Seitenlänge mit einem Volumen von V = s3 = 1000 cm3.
Wenn man den Würfel abschneidet, hat das entsprechende abgestumpfte Hexaeder eine Seitenlänge von s = 10 cm / (1 + √2) = 4,142136 cm.
Das Volumen beträgt V = (7/3) · s3 · (3 + 2·√2) = 966,498 cm3.
Wenn man den Würfel weiter abschneidet, hat das entsprechende Kuboktaeder eine Seitenlänge von s = 10 cm / √2 = 7,071068 cm.
Das Volumen beträgt V = (5/3) · s3 · √2 = 833,333 cm3.
Wenn man den Würfel noch weiter abschneidet, hat das entsprechende Oktaeder eine Seitenlänge von s = 10 cm / √2 = 7,071068 cm.
Das Volumen beträgt V = (1/3) · s3 · √2 = 166,667 cm3.
Wenn man das Oktaeder abschneidet, hat das entsprechende abgestumpfte Oktaeder eine Seitenlänge von s = 10 cm / (3 · √2) = 2,357023 cm.
Das Volumen beträgt V = 8 · s3 · √2 = 148,148 cm3.
Wenn man das Oktaeder weiter abschneidet, hat das entsprechende Kuboktaeder eine Seitenlänge von s = 10 cm / (2 · √2) = 3,535534 cm.
Das Volumen beträgt V = (5/3) · s3 · √2 = 104,167 cm3.
Wenn man das Oktaeder noch weiter abschneidet, hat der entsprechende Würfel eine Seitenlänge von s = 10 cm / 3 = 3,333333 cm.
Das Volumen beträgt V = s3 = 37,037 cm3.
Konkretes Beispiel, wie man durch Abschneiden vom Dodekaeder zum Oktaeder und dann wieder zum Dodekaeder kommt:
Ausgegangen wird von einem Dodekaeder von s = 10 cm Seitenlänge.
Wenn man das Dodekaeder abschneidet, hat das entsprechende abgestumpfte Dodekaeder eine Seitenlänge von s = 10 cm · cos(36°) / (1 + cos(36°)) = 4,472136 cm.
Wenn man das Dodekaeder weiter abschneidet, hat das entsprechende Ikosidodekaeder eine Seitenlänge von s = 10 cm · cos(36°) = 8,090170 cm.
Wenn man das Dodekaeder noch weiter abschneidet, hat das entsprechende Ikosaeder eine Seitenlänge von s = 10 cm · √(250 + 110·√5) / (5 · √(10 + 2·√5)) = 11,708204 cm.
Wenn man das Ikosaeder abschneidet, hat das entsprechende abgestumpfte Ikosaeder eine Seitenlänge von s = 11,708204 cm / 3 = 3,902735 cm.
Wenn man das Ikosaeder weiter abschneidet, hat das entsprechende Ikosidodekaeder eine Seitenlänge von s = 11,708204 cm / 2 = 5,854102 cm.
Wenn man das Ikosaeder noch weiter abschneidet, hat das entsprechende Dodekaeder eine Seitenlänge von s = 11,708204 cm · (3 + √5) / (3 · (1 + √5)) = 6,314757 cm.
Erzeugung von archimedischen Körper aus archimedischen und catalanischen (dual-archimedischen) Körpern
Entfernt man bei einem abgestumpften Hexaeder die gleichseitigen Dreiecke und zieht die regelmäßigen Achtecke so weit auseinander,
dass Quadrate und regelmäßige Sechsecke in die Lücken passen, dann erhält man ein abgestumpftes Kuboktaeder.
Entfernt man bei einem abgestumpften Dodekaeder die gleichseitigen Dreiecke und zieht die regelmäßigen Zehnecke so weit auseinander,
dass Quadrate und regelmäßige Sechsecke in die Lücken passen, dann erhält man ein abgestumpftes Ikosidodekaeder.
Durch Abschneiden der Ecken des Kuboktaeders lässt sich nicht das abgestumpfte Kuboktaeder erzeugen!
Durch Abschneiden der Ecken des Ikosidodekaeders lässt sich nicht das abgestumpfte Ikosidodekaeder erzeugen!
In beiden Fällen entstehen nämlich Rechtecke statt Quadrate. Die Namen sind also irreführend.
Für die Erzeugung eines abgeschrägten Hexaeders oder abgeschrägten Dodekaeders gibt es leider kein einfaches und anschauliches Verfahren.
Schneidet man von einem Rhombendodekaeder die 14 Ecken so ab, dass neben 6 Quadraten und 8 gleichseitigen Dreiecken aus den 12 Rauten
weitere 12 Quadrate entstehen, erhält man ein Rhombenkuboktaeder.
Schneidet man von einem Rhombentriakontaeder die 32 Ecken so ab, dass neben 20 gleichseitigen Dreiecken und 12 regelmäßigen Fünfecken
aus den 30 Rauten 30 Quadrate entstehen, erhält man ein Rhombenikosidodekaeder.
Die folgenden Tabellen gelten für platonische Körper und archimedische Körper im dreidimensionalen Raum. Die Sphärizität (Kugelähnlichkeit)
in der ersten Tabelle ist definiert als "die Oberfläche einer Kugel gleichen Volumens geteilt durch die Oberfläche des
entsprechenden Polyeders". Archimedische Körper besitzen keine eindeutig definierten Inkugeln, da zu den verschiedenen Sorten
von regelmäßigen Vielecken eines archimedischen Körpers Inkugeln unterschiedlicher Radien gehören, die allerdings alle
den gleichen Mittelpunkt besitzen. In der letzten Tabelle ist mit Inkugelradius bei den archimedischen Körpern
deshalb der kleinste Radius der Inkugeln gemeint. Er gehört zu den regelmäßigen Vielecken mit den meisten Ecken.
| | | | | |
| | | | | |
| Polyeder | Summe | Anzahl | Anzahl | Anzahl | Sphärizität |
| (Platonische Körper, | der Winkel | und Art | der | der | (Kugel- |
| Archimedische Körper) | an jeder | der | Ecken | Kanten | ähnlichkeit) |
| | Ecke | Flächen | | | |
| | | | | |
| Tetraeder | 180° | 4 Dreiecke | 4 | 6 | 0,671139 |
| Hexaeder (Würfel) | 270° | 6 Quadrate | 8 | 12 | 0,805996 |
| Oktaeder | 240° | 8 Dreiecke | 6 | 12 | 0,845583 |
| Dodekaeder | 324° | 12 Fünfecke | 20 | 30 | 0,910453 |
| Ikosaeder | 300° | 20 Dreiecke | 12 | 30 | 0,939326 |
| | | | | | |
| | | | | | |
| abgestumpftes Tetraeder | 300° | 4 Dreiecke, 4 Sechsecke | 12 | 18 | 0,775413 |
| | | | | | |
| abgestumpftes Hexaeder | 330° | 8 Dreiecke, 6 Achtecke | 24 | 36 | 0,849494 |
| | | | | | |
| abgestumpftes Oktaeder | 330° | 6 Quadrate, 8 Sechsecke | 24 | 36 | 0,909918 |
| | | | | | |
| abgestumpftes Dodekaeder | 348° | 20 Dreiecke, 12 Zehnecke | 60 | 90 | 0,926012 |
| | | | | | |
| abgestumpftes Ikosaeder | 348° | 12 Fünfecke, 20 Sechsecke | 60 | 90 | 0,966622 |
| (Fußballkörper) | | | | | |
| | | | | | |
| Kuboktaeder | 300° | 8 Dreiecke, 6 Quadrate | 12 | 24 | 0,904997 |
| | | | | | |
| Ikosidodekaeder | 336° | 20 Dreiecke, 12 Fünfecke | 30 | 60 | 0,951024 |
| | | | | | |
| Rhombenkuboktaeder | 330° | 8 Dreiecke, 18 Quadrate | 24 | 48 | 0,954080 |
| (kleines Rhombenkuboktaeder) | | | | | |
| | | | | | |
| abgestumpftes Kuboktaeder | 345° | 12 Quadrate, 8 Sechsecke | 48 | 72 | 0,943166 |
| (großes Rhombenkuboktaeder) | | 6 Achtecke | | | |
| | | | | | |
| Rhombenikosidodekaeder | 348° | 20 Dreiecke, 30 Quadrate | 60 | 120 | 0,979237 |
| (kleines Rhombenikosidodekaeder) | | 12 Fünfecke | | | |
| | | | | | |
| abgestumpftes Ikosidodekaeder | 354° | 30 Quadrate, 20 Sechsecke | 120 | 180 | 0,970313 |
| (großes Rhombenikosidodekaeder) | | 12 Zehnecke | | | |
| | | | | | |
| abgeschrägtes Hexaeder | 330° | 32 Dreiecke, 6 Quadrate | 24 | 60 | 0,965196 |
| | | | | | |
| abgeschrägtes Dodekaeder | 348° | 80 Dreiecke, 12 Fünfecke | 60 | 150 | 0,982011 |
| | | |
| | | |
| Polyeder mit | Volumen | Oberfläche |
| Kantenlänge s | | |
| (Platonische Körper, | | |
| Archimedische Körper) | | |
| | | |
| Tetraeder | (1/12) · s3 · √2 | s2 · √3 |
| Hexaeder | s3 | 6 · s2 |
| Oktaeder | (1/3) · s3 · √2 | 2 · s2 · √3 |
| Dodekaeder | (1/4) · s3 · (15 + 7·√5) | 3 · s2 · √(25 + 10·√5) |
| Ikosaeder | (5/12) · s3 · (3 + √5) | 5 · s2 · √3 |
| | | |
| | | |
| abgestumpftes Tetraeder | (23/12) · s3 · √2 | 7 · s2 · √3 |
| | |
| abgestumpftes Hexaeder | (7/3) · s3 · (3 + 2·√2) | 2 · s2 · (6 + 6·√2 + √3) |
| | |
| abgestumpftes Oktaeder | 8 · s3 · √2 | 6 · s2 · (1 + 2·√3) |
| | |
| abgestumpftes Dodekaeder | (5/12) · s3 · (99 + 47·√5) | 5 · s2 · (√3 + 6·√(5 + 2·√5)) |
| abgestumpftes Ikosaeder | (1/4) · s3 · (125 + 43·√5) | 3 · s2 · (10·√3 + √(25 + 10·√5)) |
| (Fußballkörper) | | |
| | |
| Kuboktaeder | (5/3) · s3 · √2 | 2 · s2 · (3 + √3) |
| | | |
| Ikosidodekaeder | (1/6) · s3 · (45 + 17·√5) | s2 · (5·√3 + 3·√(25 + 10·√5)) |
| | |
| Rhombenkuboktaeder | (2/3) · s3 · (6 + 5·√2) | 2 · s2 · (9 + √3) |
| (kleines Rhombenkuboktaeder) | | |
| abgestumpftes Kuboktaeder | 2 · s3 · (11 + 7·√2) | 12 · s2 · (2 + √2 + √3) |
| (großes Rhombenkuboktaeder) | | |
| | |
| Rhombenikosidodekaeder | (1/3) · s3 · (60 + 29·√5) | s2 · (30 + 5·√3 + 3·√(25 + 10·√5)) |
| (kleines Rhombenikosidodekaeder) | | |
| | |
| abgestumpftes Ikosidodekaeder | 5 · s3 · (19 + 10·√5) | 30 · s2 · (1 + √3 + √(5 + 2·√5)) |
| (großes Rhombenikosidodekaeder) | | |
| | |
| abgeschrägtes Hexaeder | 7,889477 · s3 | 2 · s2 · (3 + 4·√3) |
| | |
| abgeschrägtes Dodekaeder | 37,616649 · s3 | s2 · (20·√3 + 3·√(25 + 10·√5)) |
| | |
| | | | |
| | | | |
| Polyeder mit | Umkugel- | Inkugel- | Inkugel- |
| Kantenlänge s | radius | radius | radius*/ |
| (Platonische Körper, | | | Umkugel- |
| Archimedische Körper) | | | radius |
| | | | |
| Tetraeder | (1/4) · s · √6 | (1/12) · s · √6 | 0,333333 |
| Hexaeder | (1/2) · s · √3 | (1/2) · s | 0,577350 |
| Oktaeder | (1/2) · s · √2 | (1/6) · s · √6 | 0,577350 |
| Dodekaeder | (1/4) · s · √3 · (1 + √5) | (1/20) · s · √(250 + 110·√5) | 0,794654 |
| Ikosaeder | (1/4) · s · √(10 + 2·√5) | (1/12) · s · √3 · (3 + √5) | 0,794654 |
| | | | |
| | | | |
| abgestumpftes Tetraeder | (1/4) · s · √22 | (1/4) · s · √6 | 0,522233 |
| | | |
| abgestumpftes Hexaeder | (1/2) · s · √(7 + 4·√2) | (1/2) · s · (1 + √2) | 0,678598 |
| | | |
| abgestumpftes Oktaeder | (1/2) · s · √10 | (1/2) · s · √6 | 0,774597 |
| | | |
| abgestumpftes Dodekaeder | (1/4) · s · √(74 + 30·√5) | (1/4) · s · √(50 + 22·√5) | 0,838505 |
| | | |
| abgestumpftes Ikosaeder | (1/4) · s · √(58 + 18·√5) | (1/4) · s · √3 · (3 + √5) | 0,914958 |
| (Fußballkörper) | | | |
| Kuboktaeder | s | (1/2) · s · √2 | 0,707107 |
| | | |
| Ikosidodekaeder | (1/2) · s · (1 + √5) | (1/5) · s · √(25 + 10·√5) | 0,850651 |
| | | |
| Rhombenkuboktaeder | (1/2) · s · √(5 + 2·√2) | (1/2) · s · (1 + √2) | 0,862856 |
| (kleines Rhombenkuboktaeder) | | | |
| abgestumpftes Kuboktaeder | (1/2) · s · √(13 + 6·√2) | (1/2) · s · (1 + 2·√2) | 0,825943 |
| (großes Rhombenkuboktaeder) | | | |
| | | |
| Rhombenikosidodekaeder | (1/2) · s · √(11 + 4·√5) | (3/10) · s · √(25 + 10·√5) | 0,924594 |
| (kleines Rhombenikosidodekaeder) | | | |
| | | |
| abgestumpftes Ikosidodekaeder | (1/2) · s · √(31 + 12·√5) | (1/2) · s · √(25 + 10·√5) | 0,904944 |
| (großes Rhombenikosidodekaeder) | | | |
| | | |
| abgeschrägtes Hexaeder | 1,343713 · s | 1,142614 · s | 0,850340 |
| | | |
| abgeschrägtes Dodekaeder | 2,155837 · s | 1,980916 · s | 0,918861 |
| | | |
Kugelähnlichkeit von platonischen Körpern und archimedischen Körpern*
Welcher platonische Körper oder archimedische Körper hat nun die größte Kugelähnlichkeit (Sphärizität)? Diese Frage
lässt sich nicht so exakt beantworten, wie man zunächst vermutet. Das liegt an der komplexen Eigenschaft der Kugelähnlichkeit,
die man auf verschiedene Weise sinnvoll definieren kann. Da platonische Körper und archimedische Körper jeweils gleichartige
Ecken besitzen, kann man die Winkelsumme der an einer Ecke zusammenstoßenden Vielecke als Kriterium verwenden. Danach ist die
Kugelähnlichkeit dieser Polyeder umso größer, je näher diese Winkelsumme bei 360° liegt. Nach dieser Definition hat das
Dodekaeder unter den platonischen Körpern mit einer Winkelsumme von 324° die größte Kugelähnlichkeit. Unter den
archimedischen Körper ist es das abgestumpfte Ikosidodekaeder mit 354°. Diese einfache Definition ist nur dann einigermaßen
sinnvoll, wenn die Flächen der aneinanderstoßenden Vielecke nicht zu verschieden sind. Beispielsweise werden Prismen einer Kugel immer
unähnlicher, wenn die Eckenzahl der beiden gegenüberliegenden regelmäßigen Vielecke zunimmt, ihre Fläche also im Vergleich zu
den Quadraten des Prismas immer größer wird. Die Winkelsumme nähert sich dagegen immer mehr dem Wert von 360°.
Man kann zur Definition der Kugelähnlichkeit auch das Verhältnis der Radien von Inkugel zu Umkugel verwenden. Da archimedische
Körper für jeden Typ von regelmäßigen Vielecken eine andere "Inkugel" besitzen, muss man hier diejenige mit dem kleinsten
Radius nehmen. Nach dieser anschaulichen Definition sind Dodekaeder und Ikosaeder die beiden platonischen Körper mit der größten
Kugelähnlichkeit. Ihr Radienverhältnis beträgt 0,795. Unter den archimedischen Körpern hat das Rhombenikosidodekaeder
mit einem Wert von 0,925 die größte Kugelähnlichkeit.
Eine allgemeinere und wesentlich bessere Definition für Kugelähnlichkeit ist das in der Tabelle verwendete Verhältnis
von Kugeloberfläche zu Oberfläche des betrachteten Polyeders bei gleichem Volumen beider Körper. Die Kugel besitzt ja
bei gleichem Volumen die kleinste Oberfläche aller Körper. Unter den platonischen Körpern hat nach dieser Definition
das Ikosaeder mit 0,939 den größten Wert. Von den archimedischen Körpern hat das abgeschrägte Dodekaeder mit einem Wert
von 0,982 die größte Kugelähnlichkeit. Diese Definition lässt sich auch auf andere Polyeder anwenden.
Würfeln mit platonischen Körpern und archimedischen Körpern
Alle 5 platonischen Körper eignen sich gut als "Würfel". Jeder dieser Körper bleibt nämlich beim Würfeln mit der
gleichen Wahrscheinlichkeit auf einer seiner n Seitenflächen liegen, so dass die Wahrscheinlichkeit für jede Fläche eines platonischen
Körper gleich 1/n ist. Beim Tetraeder gibt es allerdings das kleine Problem, dass sich dann oben keine Fläche, sondern eine
Ecke befindet.
Verwendet man einen archimedischen Körper als "Würfel", muss man beachten, dass es dort zwei oder gar drei Arten von Flächen
gibt, auf denen der Körper mit unterschiedlicher Wahrscheinlichkeit liegenbleiben kann. Drei Arten von Flächen besitzen zunächst
das Rhombenikosidodekaeder, das abgestumpfte Kuboktaeder und das abgestumpfte Ikosidodekaeder. Das Gleiche gilt aber auch
für das Rhombenkuboktaeder, das abgeschrägte Hexaeder und das abgeschrägte Dodekaeder. Das Rhombenkuboktaeder besitzt
nämlich Quadrate mit 2 und mit 4 Quadraten als Nachbarn. Und die beiden abgeschrägten Körper besitzen Dreiecke mit 2 und
mit 3 Dreiecken als Nachbarn. Wenn diese beiden Körper auf Dreiecken liegenbleiben, die nur 2 Dreiecke als Nachbarn haben,
dann befinden sich außerdem oben Ecken. Bei den übrigen 7 archimedischen Körpern gibt es dagegen nur zwei Arten von Flächen,
auf denen die Körper mit jeweils unterschiedlichen Wahrscheinlichkeiten liegenbleiben können. Beim abgestumpften Tetraeder gibt es
allerdings das kleine Problem, dass die Fläche, auf der er liegenbleibt, von anderer Art ist als die, die sich dann oben befindet.
Die Wahrscheinlichkeiten für die verschiedenen Flächen eines archimedischen Körpers lassen sich nicht auf einfache Weise berechnen.
Sie hängen nicht nur von der Anzahl und Größe dieser Flächen ab.
Ein gewisses Gefühl dafür bekommt man, wenn man sich den im Großen Tipp-Kick-Buch von Katrin Höfer und Peter Hesse erwähnten
empirischen Versuch anschaut (Seite 119). In dem Versuch wurde 15.000-mal ein Kuboktaeder mit seinen 8 Dreiecken und 6 Quadraten
geworfen. Dabei blieb er in 23,2% der Fälle auf einem Dreieck liegen, obwohl der Flächenanteil der Dreiecke immerhin
2·√3 / (6 + 2·√3) = 36,6% beträgt. Anders ausgedrückt, bleibt das Kuboktaeder nur in 23,2% / 36,6% = 63,4%
der Fälle, die man aufgrund des Flächenanteils der Dreiecke erwarten würde, auf irgendeinem Dreieck liegen.
Weitere konvexe Polyeder
Eine weitere Gruppe von konvexen Polyedern sind die Johnson-Körper.
Sie sind ebenfalls nur aus regelmäßigen Vielecken aufgebaut, gehören aber weder zu den 5 platonischen Körpern oder
13 archimedischen Körpern noch zu den unendlich vielen Prismen oder Antiprismen. Es gibt 92 derartige Polyeder.
Zu ihnen gehört auch das Pseudo-Rhombenkuboktaeder, eine Variante des Rhombenkuboktaeders.
Die catalanischen Körper sind die zu den archimedischen Körpern dualen Polyeder.
Deshalb heißen sie auch dual-archimedische Körper. Catalanische Körper haben nur
eine Sorte von Vielecken auf ihrer Oberfläche und besitzen eine eindeutig definierte Inkugel.
Die Doppelpyramiden oder Bipyramiden und die Deltoeder
sind die zu den Prismen bzw. Antiprismen dualen Körper. Sie besitzen deckungsgleiche gleichschenklige Dreiecke bzw.
Drachenvierecke auf ihrer Oberfläche. Die Deltoeder gehören zur Gruppe der Trapezoeder, die alle von kongruenten
Vierecken begrenzt werden.
Deltaeder sind nur von gleichseitigen Dreiecken begrenzte Polyeder. Es gibt insgesamt
8 konvexe Deltaeder, zu denen auch das Tetraeder, Oktaeder, Ikosaeder, die von gleichseitigen Dreiecken begrenzten
Dreiecks- und Fünfecksdoppelpyramiden sowie drei weitere Johnson-Körper gehören.
Ein Rhomboeder ist ein spezielles Parallelepiped (Spat), das sechs deckungsgleiche Rauten auf
seiner Oberfläche besitzt. Das Dürer-Polyeder ist ein an zwei gegenüberliegenden Ecken
abgestumpftes Rhomboeder. Es besteht aus 6 deckungsgleichen und achsensymmetrischen Fünfecken und zwei gleichseitigen Dreiecken,
und es besitzt eine Umkugel.
Geodätische Kuppeln bestehen nur aus Dreiecken, die nicht gleichseitig zu sein brauchen.
Diese Körper besitzen eine eindeutig definierte Umkugel. Entsprechend gibt es auch
die zu den geodätischen Kuppeln dualen Polyeder.
Das Mathematik-Rätsel über Würfelschnitte enthält auch alle Schnitte durch platonische Körper,
bei denen regelmäßige Vielecke als Schnittflächen entstehen. Schließlich enthält ein weiteres Mathematik-Rätsel alle
platonischen Körper, die man platonischen Körpern einbeschreiben kann.
Reguläre nichtkonvexe Polyeder
Neben den 5 regulären konvexen Polyedern (platonische Körper) gibt es noch 4 reguläre nichtkonvexe Polyeder.
Dabei handelt es sich um die regulären Sternpolyeder (Sternkörper). Sie sind nur aus regelmäßigen
konvexen Vielecken oder aus regulären Sternpolygonen aufgebaut. Als Kanten der Sternpolyeder gelten die geraden Verbindungen
zwischen zwei benachbarten Spitzen, wobei diese Verbindungen auch teilweise durch den Körper gehen können. Über diese Verbindungen
lassen sich von einer Spitze aus alle anderen Spitzen erreichen. Die Spitzen eines Körpers sehen alle gleich aus und liegen auf einer
Umkugel.
Ein Dodekaederstern (Kleines Sterndodekaeder) entsteht durch Verlängerung der Kanten eines
Dodekaeders über seine Ecken hinaus. Der Dodekaederstern wird von 12 Pentagrammen begrenzt. Die Spitzen des Dodekaedersterns
kann man als Ecken eines Ikosaeders auffassen.
Ein Ikosaederstern (Großes Sterndodekaeder) entsteht durch Verlängerung der Kanten eines
Ikosaeders über seine Ecken hinaus. Der Ikosaederstern wird von 12 Pentagrammen begrenzt. Die Spitzen des Ikosaedersterns
kann man als Ecken eines Dodekaeders auffassen.
Ein Großes Dodekaeder ist quasi ein reduziertes "ausgeschabtes" Ikosaeder. Das Große Dodekaeder
wird von 12 regelmäßigen Fünfecken begrenzt. Die Spitzen des Großen Dodekaeders kann man als Ecken eines Ikosaeders auffassen.
Ein Großes Ikosaeder ist quasi ein reduzierter "ausgeschabter" Dodekaederstern. Das Große Ikosaeder
wird von 20 gleichseitigen Dreiecken begrenzt. Die Spitzen des Großen Ikosaeders kann man als Ecken eines Ikosaeders auffassen.
Ein Oktaederstern (Sterntetraeder) ist kein reguläres Sternpolyeder, weil man über die Kanten von einer Spitze aus nicht
alle anderen Spitzen erreichen kann. Er wird deshalb auch als regulärer Sternpseudopolyeder bezeichnet. Ein Oktaederstern entsteht
durch das Aufsetzen von Tetraedern auf die Flächen eines Oktaeders und gehört deshalb zu den nichtkonvexen Deltaedern. Man kann ihn auch
als Verschmelzung zweier Tetraeder auffassen.
Ein Hexaederstern (Pyramidenwürfel) und ein Tetraederstern sind erst recht keine regulären Sternpolyeder.
Bei Ihnen kann man noch nicht einmal von einer Spitze auf einer Kante entlang auf geradem Wege eine andere Spitze erreichen.
Das Mathematik-Rätsel über Würfelschnitte enthält auch alle Schnitte durch platonische Körper,
bei denen regelmäßige Vielecke als Schnittflächen entstehen. Schließlich enthält ein weiteres Mathematik-Rätsel alle
platonischen Körper, die man platonischen Körpern einbeschreiben kann.
Links zum Thema:
Wikipedia: Archimedischer Körper - Wikipedia
Gijs Korthals Altes: Paper Models of Polyhedra
Jürgen Köller: Archimedische Körper
Arndt Brünner: Platonische Körper und Archimedische Körper
Referenz: Reguläre und halbreguläre Polyeder (Tiberiu Roman, Deutsch Taschenbücher, Band 56)
Copyright © Werner Brefeld (1999)

