Platonische und Archimedische Parkettierungen

Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum, Themenübersicht auf der Hauptseite:

Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben

Während platonische Parkettierungen nur regelmäßige Vielecke einer Sorte besitzen, haben archimedische Parkettierungen regelmäßige Vielecke von mehr als einer Sorte. Außerdem dürfen hier die Eckpunkte der Vielecke nur mit den Eckpunkten der anderen Vielecke zusammenstoßen. Und an jedem Punkt, an dem die Vielecke zusammenstoßen, muss Anordnung der Vielecke gleich sein. Es gibt 3 platonische Parkettierungen und 8 archimedische Parkettierungen, wobei erwähnt werden sollte, dass die archimedische Parkettierung 3-3-3-3-6 in zwei spiegelbildlich entgegengesetzten Varianten auftritt. Die folgende Abbildung zeigt die 3 platonischen Parkettierungen und die 8 archimedischen Parkettierungen:

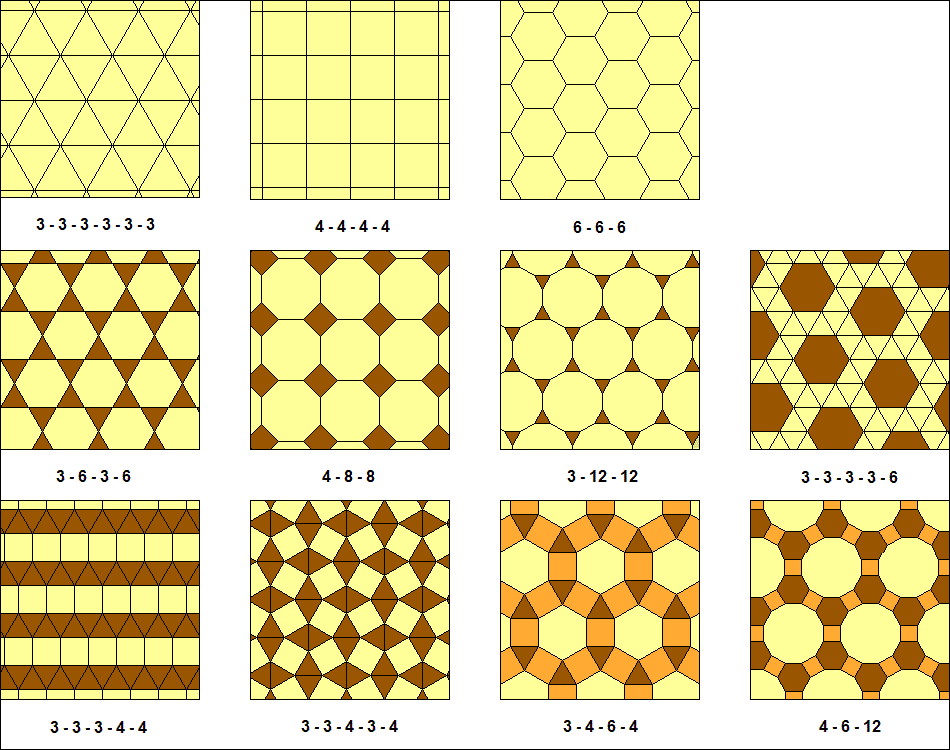
Die Bezeichnungen geben an, welche n-Ecke in welcher Abfolge bei der jeweiligen Parkettierung zusammenstoßen, wobei mit den kleinsten n-Eck begonnen wird. Dass es nicht mehr Parkettierungen dieser Art gibt, kann man durch Betrachtung der Anordnung und der Innenwinkel der zusammenstoßenden Vielecke zeigen. Es müssen ja an jedem Punkt mindestens 3 Vielecke zusammenstoßen und die Summe ihrer zusammenstoßenden Innenwinkel muss gleich 360° sein. Daraus folgt, dass es nur 3 platonische Parkettierungen geben kann, weil man nur 6 gleichseitige Dreiecke, 4 Quadrate oder 3 regelmäßige Sechsecke unter den angegebenen Bedingungen zusammenfügen kann.

Überträgt man diese Überlegungen auf Parkettierungen im dreidimensionalen Raum, so muss man platonische und archimedische Körper suchen, die den Raum lückenlos füllen können. Das trifft auf die folgenden Fälle zu, wobei jeweils die Anzahl der Polyeder angegeben ist, deren Ecken an einem Punkt zusammenstoßen:

8 Würfel
4 abgestumpfte Oktaeder
8 Tetraeder + 6 Oktaeder
4 Kuboktaeder + 2 Oktaeder
4 abgestumpfte Würfel + 1 Oktaeder
6 abgestumpfte Tetraeder + 2 Tetraeder
3 Rhombenkuboktaeder + 1 Würfel + 1 Tetraeder
2 Rhombenkuboktaeder + 2 Würfel + 1 Kuboktaeder
2 abgestumpfte Oktaeder + 2 abgestumpfte Tetraeder + 1 Kuboktaeder
2 abgestumpfte Kuboktaeder + 1 abgestumpftes Oktaeder + 1 Würfel
2 abgestumpfte Kuboktaeder + 1 abgestumpfter Würfel + 1 abgestumpftes Tetraeder

Außerdem ist noch bemerkenswert, dass es unter den platonischen Körpern, den archimedischen Körpern und den catalanischen Körpern jeweils nur einen Körper gibt, mit dem man den Raum lückenlos füllen kann. Es sind das der Würfel, das abgestumpfte Oktaeder und das Rhombendodekaeder.

Erzeugung von platonischen und archimedischen Parkettierungen aus platonischen Parkettierungen

Schneidet man bei der Parkettierung 3-3-3-3-3-3 (Parkettierung aus gleichseitigen Dreiecken) die Ecken der gleichseitigen Dreiecke so ab, dass daraus regelmäßige Sechsecke werden und füllt die entstehenden Lücken mit regelmäßigen Sechsecken, so ergibt sich die Parkettierung 6-6-6 (Parkettierung aus regelmäßigen Sechsecken). Schneidet man die Ecken der Dreiecke noch weiter ab, so dass daraus wieder (allerdings kleinere) gleichseitige Dreiecke werden und füllt die größer gewordenen Lücken wieder mit regelmäßigen Sechsecken, so erhält man die Parkettierung 3-6-3-6. Schneidet man die Ecken der Dreiecke noch weiter ab, so dass die Lücken mit regelmäßigen Zwölfecken gefüllt werden können, so erhält man die Parkettierung 3-12-12. Schneidet man schließlich die Ecken der Dreiecke so weit ab, dass die Dreiecke zu einem Punkt schrumpfen, kann man die Lücken wieder mit einer Parkettierung aus regelmäßigen Sechsecken füllen, allerdings um 30° gedreht. Zieht man bei der Parkettierung 3-3-3-3-3-3 die gleichseitigen Dreiecke so weit auseinander, dass Quadrate und regelmäßige Sechsecke in die Lücken passen, erhält man die Parkettierung 3-4-6-4.

Schneidet man bei der Parkettierung 4-4-4-4 (Parkettierung aus Quadraten) die Ecken der Quadrate so ab, dass daraus regelmäßige Achtecke werden und füllt die entstehenden Lücken mit Quadraten, so ergibt sich die Parkettierung 4-8-8. Schneidet man die Ecken der Quadrate noch weiter ab, so dass aus den Quadraten wieder (allerdings kleinere) Quadrate werden und füllt die größer gewordenen Lücken wieder mit Quadraten, so erhält man wieder eine Parkettierung aus Quadraten, allerdings um 45° gedreht. Schneidet man die Ecken der Quadrate noch weiter ab, so dass die Lücken mit regelmäßigen Achtecken gefüllt werden können, so erhält man wieder die Parkettierung 4-8-8. Schneidet man schließlich die Ecken der Quadrate so weit ab, dass die Quadrate zu einem Punkt schrumpfen, kann man die Lücken wieder mit einer Parkettierung aus Quadraten füllen, dass die gleiche Orientierung hat wie die Ausgangsparkettierung.

Schneidet man bei der Parkettierung 6-6-6 (Parkettierung aus regelmäßigen Sechsecken) die Ecken der regelmäßigen Sechsecke so ab, dass daraus regelmäßige Zwölfecke werden und füllt die entstehenden Lücken mit gleichseitigen Dreiecken, so ergibt sich die Parkettierung 3-12-12. Schneidet man die Ecken der Sechsecke noch weiter ab, so dass aus den Sechsecken wieder (allerdings kleinere) regelmäßige Sechsecke werden und füllt die größer gewordenen Lücken wieder mit gleichseitigen Dreiecken, so erhält man die Parkettierung 3-6-3-6. Schneidet man die Ecken der Sechsecke noch weiter ab, so dass die Lücken mit regelmäßigen Sechsecken gefüllt werden können, so erhält man wieder eine Parkettierung aus regelmäßigen Sechsecken, allerdings um 30° gedreht. Schneidet man schließlich die Ecken der Sechsecke so weit ab, dass die Sechsecke zu einem Punkt schrumpfen, kann man die Lücken mit einer Parkettierung aus regelmäßigen Dreiecken füllen. Zieht man bei der Parkettierung 6-6-6 die regelmäßigen Sechsecke so weit auseinander, dass gleichseitige Dreiecke und Quadrate in die Lücken passen, erhält man die Parkettierung 3-4-6-4.

Erzeugung einer weiteren archimedischen Parkettierung aus einer archimedischen Parkettierung

Entfernt man bei der Parkettierung 3-12-12 die gleichseitigen Dreiecke und zieht die regelmäßigen Zwölfecke so weit auseinander, dass Quadrate und regelmäßige Sechsecke in die Lücken passen,
erhält man die Parkettierung 4-6-12.

Erzeugung von platonischen Parkettierungen aus platonischen Körpern
(siehe dazu die Web-Seite über platonische und archimedische Körper)

Trennt man die Oberfläche eines Ikosaeders auf und fügt an jeder Ecke ein weiteres (sechstes) gleichseitiges Dreieck hinzu,
erhält man die Parkettierung 3-3-3-3-3-3 (Parkettierung aus gleichseitigen Dreiecken).

Trennt man die Oberfläche eines Würfels auf und fügt an jeder Ecke ein weiteres (viertes) Quadrat hinzu,
erhält man die Parkettierung 4-4-4-4 (Parkettierung aus Quadraten).

Trennt man die Oberfläche eines Dodekaeders auf und ersetzt an jeder Ecke die 3 regelmäßigen Fünfecke durch 3 regelmäßige Sechsecke,
erhält man die Parkettierung 6-6-6 (Parkettierung aus regelmäßigen Sechsecken).

Erzeugung von archimedischen Parkettierungen aus archimedischen Körpern
(siehe dazu die Web-Seite über platonische und archimedische Körper)

Trennt man die Oberfläche eines abgestumpften Oktaeders auf und ersetzt an jeder Ecke die beiden regelmäßigen Sechsecke durch regelmäßige Achtecke,
erhält man die Parkettierung 4-8-8.

Trennt man die Oberfläche eines abgestumpften Dodekaeders auf und ersetzt an jeder Ecke die beiden regelmäßigen Zehnecke durch regelmäßige Zwölfecke,
erhält man die Parkettierung 3-12-12.

Trennt man die Oberfläche eines abgeschrägten Würfels auf und ersetzt an jeder Ecke ein dem Quadrat benachbartes Dreieck durch ein Quadrat,
erhält man die Parkettierung 3-3-3-4-4.

Trennt man die Oberfläche eines abgeschrägten Würfels auf und ersetzt an jeder Ecke ein dem Quadrat schräg gegenüber liegendes Dreieck durch ein Quadrat,
erhält man die Parkettierung 3-3-4-3-4.

Trennt man die Oberfläche eines Ikosidodekaeders auf und ersetzt an jeder Ecke die beiden regelmäßigen Fünfecke durch regelmäßige Sechsecke,
erhält man die Parkettierung 3-6-3-6.

Trennt man die Oberfläche eines Rhombenikosidodekaeders auf und ersetzt an jeder Ecke das regelmäßige Fünfeck durch ein regelmäßiges Sechseck,
erhält man die Parkettierung 3-4-6-4.

Trennt man die Oberfläche eines abgestumpften Ikosidodekaeders auf und ersetzt an jeder Ecke das regelmäßige Zehneck durch ein regelmäßiges Zwölfeck,
erhält man die Parkettierung 4-6-12.

Trennt man die Oberfläche eines abgeschrägten Dodekaeders auf und ersetzt an jeder Ecke das regelmäßige Fünfeck durch ein regelmäßiges Sechseck,
erhält man die Parkettierung 3-3-3-3-6.