 |
Sechsecke im Kreis
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite: |
36. Platziert man in einen Kreis ein einbeschriebenes regelmäßiges Sechseck, so bedeckt es 82,7% der Kreisfläche. Vergrößert man diesen Kreis, so passen immer mehr parkettartig angeordnete regelmäßige Sechsecke vollständig hinein, wobei sich das erste Sechseck weiterhin in der Mitte des Kreises befinden soll. Ab welcher Anzahl bedecken diese Sechsecke zum ersten Mal mehr als 82,7% der Kreisfläche?
Bei Cerenkov-Teleskopen und großen optischen Spiegelteleskopen setzt man die Spiegel aus sechseckigen Elementen zusammen, weil man die jeweiligen
Spiegel nicht mehr in einem Stück fertigen kann. Auch hier kommt es wie bei diesem Rätsel darauf an, mit den Sechsecken einen möglichst hohen
Anteil einer Kreisfläche abzudecken.
Für die folgenden Überlegungen wird die Länge einer Sechseckseite gleich 1 gesetzt. Der Abstand von zwei gegenüberliegenden Ecken eines regelmäßigen
Sechsecks beträgt dann 2 und der von zwei gegenüberliegenden Seiten √3 .
Abbildung 1:
Die Fläche des regelmäßigen Sechsecks ist gleich 3/2 · √3 und die des Umkreises gleich π. Die Bedeckung des Umkreises durch das Sechseck
beträgt demnach 3/2 · √3 / π = 82,699%.
Abbildung 2:
Die Fläche der 7 Sechsecke ist gleich 7 · 3/2 · √3 und die des Kreises gleich 7 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 7 · 3/2 · √3 / (7 · π) = 82,699%.
Sie ist also genau so groß wie bei dem einzelnen regelmäßigen Sechseck.
Abbildung 3:
Die Fläche der 13 Sechsecke ist gleich 13 · 3/2 · √3 und die des Kreises gleich 16 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 13 · 3/2 · √3 / (16 · π) = 67,193%.
Sie ist also sogar kleiner als bei dem einzelnen regelmäßigen Sechseck.
Abbildung 4:
Die Fläche der 19 Sechsecke ist gleich 19 · 3/2 · √3 und die des Kreises gleich 19 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 19 · 3/2 · √3 / (19 · π) = 82,699%.
Sie ist also genau so groß wie bei dem einzelnen regelmäßigen Sechseck.
Übrigens besitzen die 18 sechseckigen Spiegel des James-Webb-Weltraumteleskops genau die in Abbildung 4 gezeigte Anordnung.
Nur der zentrale (19.) Spiegel musste wegen der Strahlführung weggelassen werden.
Abbildung 5:
Die Fläche der 31 Sechsecke ist gleich 31 · 3/2 · √3 und die des Kreises gleich 31 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 31 · 3/2 · √3 / (31 · π) = 82,699%.
Sie ist also genau so groß wie bei dem einzelnen regelmäßigen Sechseck.
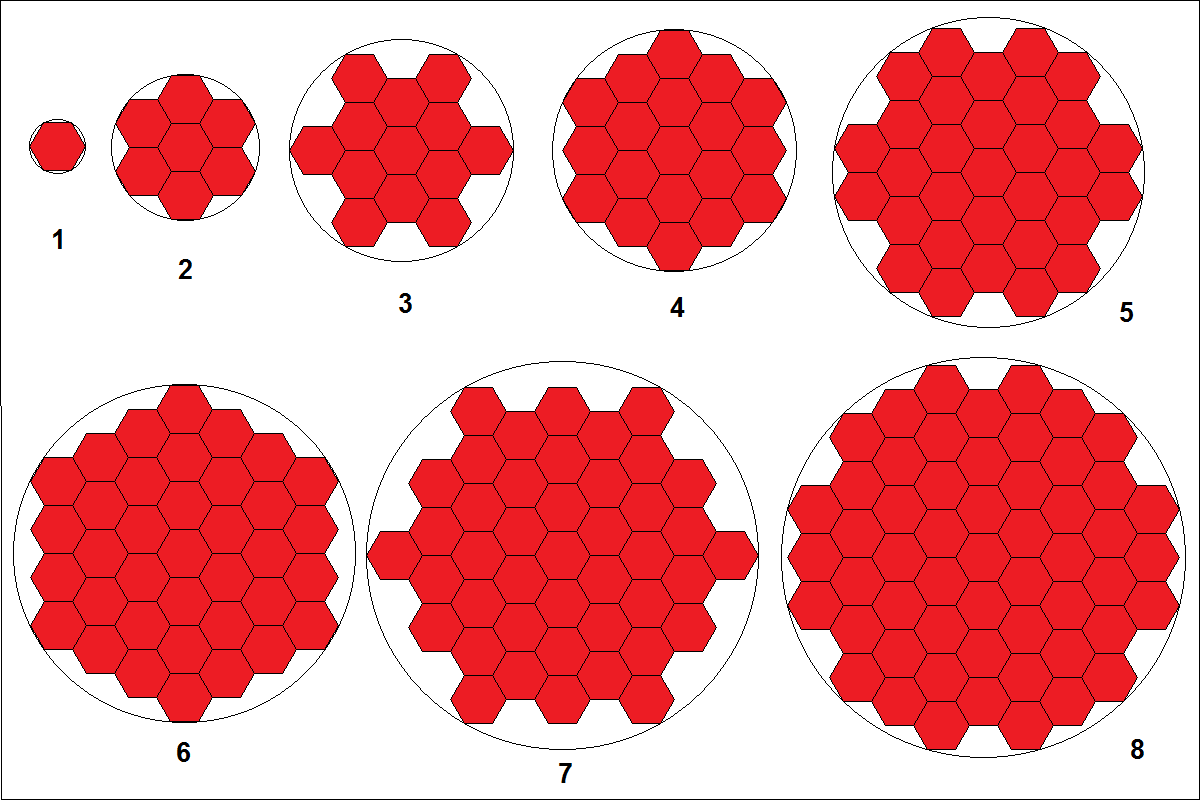
Abbildung 6:
Die Fläche der 37 Sechsecke ist gleich 37 · 3/2 · √3 und die des Kreises gleich 37 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 37 · 3/2 · √3 / (37 · π) = 82,699%.
Sie ist also genau so groß wie bei dem einzelnen regelmäßigen Sechseck.
Abbildung 7:
Die Fläche der 43 Sechsecke ist gleich 43 · 3/2 · √3 und die des Kreises gleich 49 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 43 · 3/2 · √3 / (49 · π) = 72,573%.
Sie ist also sogar kleiner als bei dem einzelnen regelmäßigen Sechseck.
Abbildung 8:
Die Fläche der 55 Sechsecke ist gleich 55 · 3/2 · √3 und die des Kreises gleich 52 · π. Die Bedeckung des Kreises durch
die Sechsecke beträgt demnach 55 · 3/2 · √3 / (52 · π) = 87,470%.
Sie ist also größer als bei dem einzelnen regelmäßigen Sechseck. Also erst 55 Sechsecke bedecken zum ersten Mal mehr als 82,7% der Kreisfläche.
Insgesamt gibt es nur 3 Anordnungen von Sechsecken, bei denen die Bedeckung des umgebenden Kreises kleiner ist als bei einem einzelnen Sechseck.
Es sind dies die Anordnungen mit 13, 43 und 97 Sechsecken. Außerdem gibt es insgesamt nur 8 Anordnungen von Sechsecken, bei denen die Bedeckung des
umgebenden Kreises genauso groß ist wie bei einem einzelnen Sechseck, und zwar bei Anordnungen mit 7, 19, 31, 37, 61, 73, 91 und 127 Sechsecken.
Die ersten 6 Anordnungen von Sechsecken, die jeweils eine größere Bedeckung des umgebenden Kreises haben als alle kleineren Anordnungen, haben
55 (87,470%), 85 (88,980%), 121 (89,345%), 151 (89,839%), 187 (89,911%) und 199 (90,924%) Sechsecke. In Klammern steht der jeweilige Bedeckungsanteil.
Wenn man die gleichen Überlegungen mit Quadraten und gleichseitigen Dreiecken anstellt, so ergibt sich als Lösung jeweils eine sehr viel kleinere
Anzahl von Flächen:
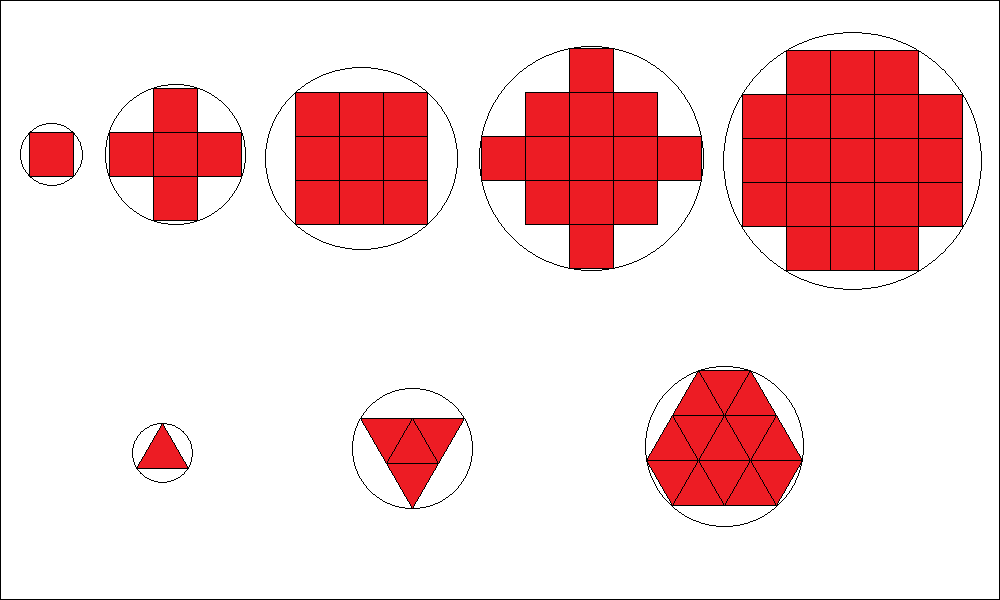
Ein Quadrat bedeckt 2 / π = 63,662% der Fläche seines Umkreises. Ebenso bedecken Parkettierungen aus 5, 9
und 13 Quadraten 2 / π = 63,662% der Fläche der kleinsten Kreise, in denen man diese Parkettierungen einschließen kann. Aber schon eine Parkettierung aus
21 Quadraten bedeckt (42/17) / π = 78,641% der entsprechenden Kreisfläche.
Ein gleichseitiges Dreieck bedeckt 3/4 · √3 / π = 41,350% der Fläche seines Umkreises. Ebenso bedeckt eine Parkettierung aus 4 gleichseitigen
Dreiecken den gleichen Anteil der Fläche des kleinsten Kreises, in dem man diese Parkettierung einschließen kann. Aber schon eine Parkettierung aus 13 gleichseitigen
Dreiecken bedeckt (39/28) · √3 / π = 76,792% der entsprechenden Kreisfläche.
Wenn man die gleichen Überlegungen mit Würfeln in einer Kugel anstellt, so ergibt sich folgende Lösung:
Ein Würfel füllt (2/√3) / π = 36,755% des Volumens seiner Umkugel aus. Die kleinste Anzahl von Würfeln, die einen größeren Anteil ihrer Umkugel
ausfüllen, beträgt 19. Ihr Anteil am Umkugelvolumen beträgt (6/√19) / π = 43,815%. Ihre Anordnung ergibt sich, wenn man 27 Würfel in Form eines
größeren Würfels anordnet und die 8 Würfel an den Ecken entfernt.
Was ist verblüffend an diesem Mathematik-Rätsel? Viele glauben intuitiv, dass man mit deutlich weniger Sechsecken auskommt, um die Bedeckung
einer Kreisfläche durch ein einzelnes regelmäßiges Sechseck zu übertreffen.
Copyright © Werner Brefeld (2020; Originalrätsel)