Platonische Körper im Würfel Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum, Themenübersicht auf der Hauptseite: Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben

34. Welche platonischen Körper können einem Würfel einbeschrieben werden?

Ein Körper ist dann einem anderen Körper einbeschrieben, wenn alle seine Ecken auf den Seitenflächen des anderen Körpers liegen. Ein Tetraeder, ein Würfel, ein Oktaeder und ein Ikosaeder kann einem Würfel einbeschrieben werden, ein Dodekaeder dagegen nicht.

Die 4 Ecken des einbeschriebenen Tetraeders liegen auf 4 der 8 Ecken des Würfels. Seine Kanten sind gleichzeitig Diagonalen der Seitenflächen des Würfels und deshalb alle gleich lang. Natürlich kann man einem Würfel auch ein Würfel einbeschreiben, indem man die 8 Ecken des einen Körpers auf die entsprechenden 8 Ecken des anderen Körpers legt. Da das Oktaeder zum Würfel dual ist, kann es einem Würfel einbeschrieben werden, indem man seine 6 Ecken auf die 6 Seitenmitten des Würfels platziert. Auf allen 6 Würfelseitenflächen liegen jeweils zwei der 12 Ecken des einbeschriebenen Ikosaeders. Die Ecken liegen auf der Mittelsenkrechten einer Kante der Seitenflächen. Das Verhältnis der Länge einer Würfelkante zur Länge einer Ikosaederkante entspricht dabei dem Goldenen Schnitt.

Dass man ein Dodekaeder dagegen nicht in einen Würfel einbeschreiben kann, lässt sich folgendermaßen begründen: Ein Dodekaeder hat 20 Ecken, ein Würfel hat 6 Seitenflächen. Auf jeder Seitenfläche des Würfels müssen im Durchschnitt also mehr als 3 Dodekaederecken liegen. 3 Ecken definieren aber eine Fläche. Wenn also 3 Dodekaederecken auf einer Würfelseitenfläche liegen, dann müssen zwangsläufig alle 5 Ecken einer Dodekaederseitenfläche auf dieser Würfelseitenfläche liegen. Es muss aber mindestens noch eine weitere Würfelseitenfläche mit 5 Dodekaederecken geben. Dies kann nur die gegenüberliegende Seitenfläche sein. Von den 20 Dodekaederecken bleiben dann noch 10 Ecken übrig. Wenn man von oben auf ein auf einer Seitenfläche liegendes Dodekaeder schaut, dann bilden diese 10 Ecken als Projektion ein regelmäßiges Zehneck. Die Ecken dieses Zehnecks müssten dann auf der Projektion der übrigen 4 Seitenflächen des Würfels, einem Quadrat, liegen. Das ist aber unmöglich, weil dann auch 3 Ecken auf einer Seite des Quadrats liegen müssten.

Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, dass es außer dem Tetraeder und dem dualen Oktaeder keine weiteren platonischen Körper gibt, die man dem Würfel einbeschreiben kann.


Neben dem Würfel gibt es noch vier weitere Platonische Körper, nämlich Tetraeder, Oktaeder, Dodekaeder und Ikosaeder. Auch diesen Polyedern kann man platonische Körper einbeschreiben. Die folgende Abbildung zeigt die möglichen Fälle für alle platonischen Körper.

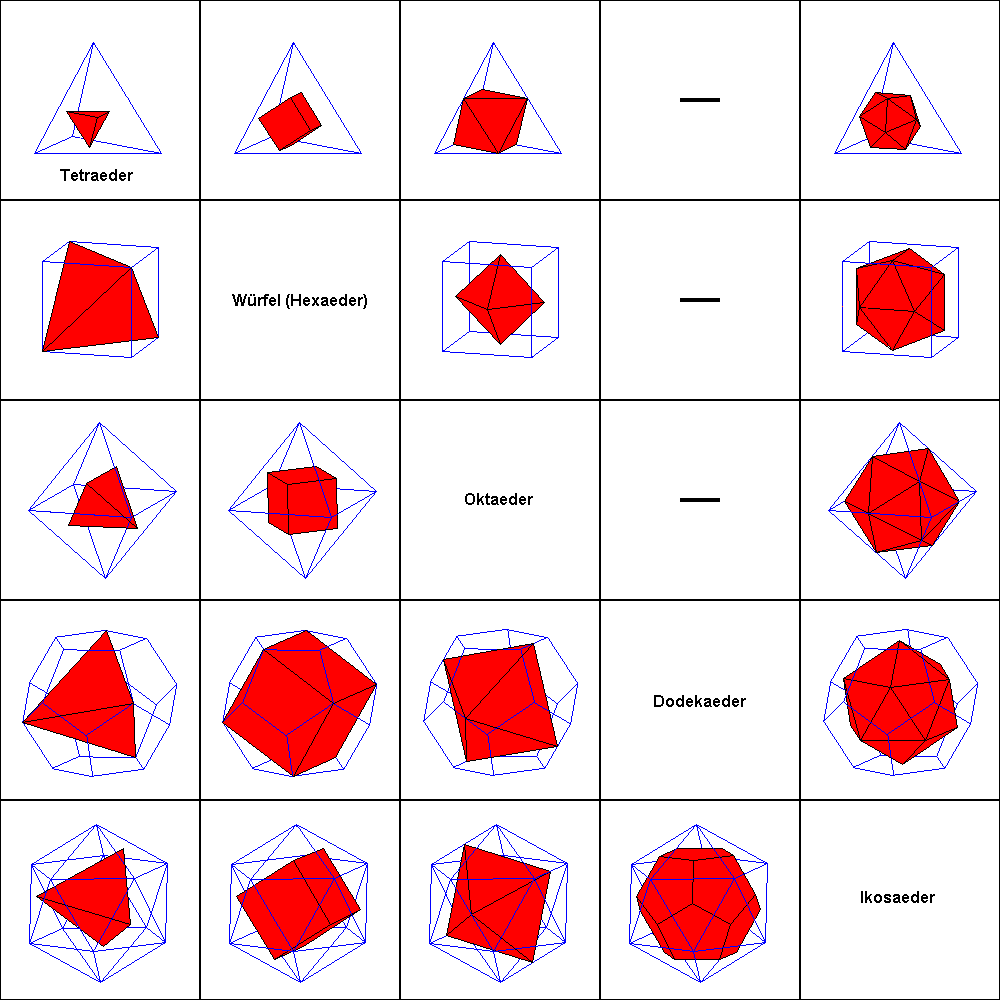
Tetraeder:
Einem Tetraeder kann man ein Tetraeder, ein Würfel, ein Oktaeder und ein Ikosaeder einbeschreiben, ein Dodekaeder dagegen nicht. Da das Tetraeder zu sich selbst dual ist, kann man einem Tetraeder auch auf nichttriviale Weise wieder ein Tetraeder einbeschreiben. Jeweils 2 der 8 Ecken des einbeschriebenen Würfels liegen auf einer der 4 Seitenflächen des Tetraeders. Diese beiden Ecken haben voneinander einen Abstand von (2 – Wurzel(2))/2 und liegen parallel zu einer Kante der entsprechenden Seitenfläche, im Abstand von (2 – Wurzel(2)) · Wurzel(3) / 4. Die Kantenlänge des Tetraeders ist hier gleich 1 gesetzt. Die 6 Ecken des einbeschriebenen Oktaeders liegen auf den Mitten der 6 Kanten des Tetraeders. Auf allen 4 Seitenflächen des Tetraeders liegen jeweils 3 der 12 Ecken des einbeschriebenen Ikosaeders. Man erhält die Positionen der Ikosaederecken, indem man die Seitenflächen des Tetraeders in 4 gleiche gleichseitige Dreiecke aufteilt und die Kanten des mittleren Dreiecks im Verhältnis des Goldenen Schnitts aufteilt.

Dass man ein Dodekaeder nicht in ein Tetraeder einbeschreiben kann, lässt sich folgendermaßen begründen: Ein Dodekaeder hat 20 Ecken, ein Tetraeder hat 4 Seitenflächen. Auf jeder Seitenfläche des Tetraeders müssten also 5 Dodekaederecken liegen. Das ist aber schon deshalb unmöglich, weil die Winkel zwischen zwei Seitenflächen bei Tetraeder und Dodekaeder unterschiedlich sind.

Oktaeder:
Einem Oktaeder kann man ein Tetraeder, ein Würfel, ein Oktaeder und ein Ikosaeder einbeschreiben, ein Dodekaeder dagegen nicht. Die 4 Ecken deseinbeschriebenen Tetraeders liegen auf 4 der 8 Seitenmitten des Oktaeders. Da der Würfel zum Oktaeder dual ist, kann er einem Oktaeder einbeschrieben werden, indem man seine 8 Ecken auf die 8 Seitenmitten des Oktaeders platziert. Die 12 Ecken des einbeschriebenen Ikosaeders liegen auf den 12 Kanten des Oktaeders. Dabei teilen die Ecken des Ikosaeders die Kanten des Oktaeders im Verhältnis des Goldenen Schnitts.

Dass man ein Dodekaeder nicht in ein Oktaeder einbeschreiben kann, lässt sich folgendermaßen begründen: Ein Dodekaeder hat 20 Ecken, ein Oktaeder hat 8 Seitenflächen. Es muss also Seitenflächen des Oktaeders mit 3 Dodekaederecken geben. 3 Ecken definieren aber eine Fläche. Wenn also 3 Ecken des Dodekaeders auf einer Seitenfläche des Oktaeders liegen, dann müssen zwangsläufig alle 5 Ecken einer Seitenfläche des Dodekaeders auf dieser Oktaederseitenfläche liegen. Es muss dann aber mindestens noch eine weitere Oktaederseitenfläche mit 5 Dodekaederecken geben. Dies kann nur die gegenüberliegende Seitenfläche sein. Von den 20 Dodekaederecken bleiben dann noch 10 Ecken übrig, von denen jeweils 5 zwei gleich große regelmäßige Fünfecke bilden, die 180° gegeneinander verdreht und parallel zueinander sind. Die Ebenen der beiden Fünfecke erzeugen beim Oktaeder als Schnittflächen zwei gleiche Sechsecke mit Innenwinkeln von 120° und abwechselnd verschiedenen Seitenlängen, die 120°, aber nicht 180° gegeneinander verdreht sind. Aus Symmetriegründen können deshalb nicht alle Ecken der beiden Fünfecke auf den Kanten dieser beiden Sechsecke liegen.

Dodekaeder:
Einem Dodekaeder kann man alle 5 platonischen Körper einbeschreiben. Die 4 Ecken des einbeschriebenen Tetraeders liegen auf 4 der 20 Ecken des Dodekaeders. Die 8 Ecken des einbeschriebenen Würfels liegen auf 8 der 20 Ecken des Dodekaeders. Die 6 Ecken des einbeschriebenen Oktaeders liegen auf 6 der 30 Kantenmitten des Dodekaeders. Da das Ikosaeder zum Dodekaeder dual ist, kann es einem Dodekaeder einbeschrieben werden, indem man seine 12 Ecken auf die 12 Seitenmitten des Dodekaeders platziert.

Ikosaeder:
Schließlich kann man einem Ikosaeder ebenfalls alle 5 platonischen Körper einbeschreiben. Die 4 Ecken des einbeschriebenen Tetraeders liegen auf 4 der 20 Seitenmitten des Ikosaeders. Die 8 Ecken des einbeschriebenen Würfels liegen auf 8 der 20 Seitenmitten des Ikosaeders. Die 6 Ecken des einbeschriebenen Oktaeders liegen auf 6 der 30 Kantenmitten des Ikosaeders. Da das Dodekaeder zum Ikosaeder dual ist, kann es einem Ikosaeder einbeschrieben werden, indem man seine 20 Ecken auf die 20 Seitenmitten des Ikosaeders platziert.


Copyright © Werner Brefeld (2011)