 |
Würfelschnitt und regelmäßige Vielecke
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite: |
19. Welche regelmäßigen Vielecke können entstehen, wenn man einen Würfel einmal durchschneidet?
Beim Schnitt durch einen Würfel werden aus den Schnitten durch die Seitenflächen des Würfels die Seiten
der Schnittfläche. Da ein Würfel 6 Seitenflächen besitzt, können deshalb beim Schneiden höchstens Sechsecke als Schnittflächen
entstehen. Weil eine Schnittfläche mindestens so viele Seiten haben muss, wie Flächen an einer Ecke des Würfels zusammenstoßen,
sind die Schnittflächen beim Würfel mindestens Dreiecke. Wie die Abbildungen zeigen, kann man tatsächlich gleichseitige Dreiecke,
Quadrate und regelmäßige Sechsecke erzeugen.
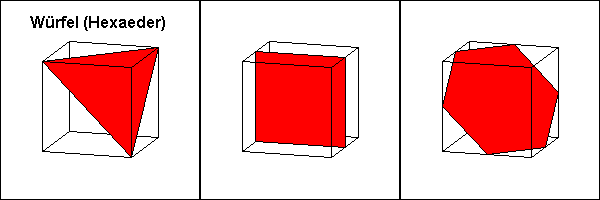
Das dargestellte Dreieck ist gleichseitig, weil alle seine Seiten mit einer Diagonalen eines Oberflächenquadrates
identisch und damit gleich sind.
Dass es sich in der mittleren Abbildung um ein Quadrat handelt, ist offensichtlich.
Wenn man die Schnittebene so legt, dass sie 5 Flächen des Würfels schneidet, ergibt sich als Schnittfläche ein Fünfeck.
Man kann dann allerdings nicht vermeiden, dass Würfelflächen geschnitten werden, die einander gegenüber liegen.
Da diese Flächen zueinander parallel sind, sind es auch die durch den Schnitt entstehenden Seiten des Fünfecks.
Man kann deshalb kein regelmäßiges Fünfeck erzeugen, da dieses keine parallelen Seiten besitzt.
Da auch beim regelmäßigen Dreieck keine zwei Seiten zueinander parallel sind, dürfen hier die geschnittenen Würfelflächen
einander nicht gegenüber liegen. Man kann das in der Zeichnung auch sehr gut erkennen.
Beim Sechseck kann man mit Hilfe des Pythagoras-Satzes leicht erkennen, dass alle Seiten gleich lang sind
und dass auch alle Abstände der Eckpunkte zum Mittelpunkt des Würfels dieselbe Länge haben.
Das Sechseck besteht also aus 6 gleichseitigen Dreiecken. Da außerdem die Verbindungslinien der jeweils gegenüberliegenden
Eckpunkte des Sechsecks durch den Mittelpunkt des Würfels gehen, handelt es sich um ein ebenes regelmäßiges Sechseck.
Was ist verblüffend an diesem Mathematik-Rätsel? Intuitiv glauben viele, dass beim Durchschneiden eines Würfels
Quadrate die einzigen regelmäßigen Vielecke sind, die entstehen können. Gleichseitige Dreiecke oder gar regelmäßige Sechsecke
hält die Intuition nicht für möglich.
Neben dem Würfel gibt es noch vier weitere platonische Körper, nämlich Tetraeder, Oktaeder, Dodekaeder und Ikosaeder.
Auch diese Polyeder kann man so durchschneiden, dass unterschiedliche regelmäßige Vielecke entstehen.
Die folgende Abbildung zeigt die möglichen Fälle für alle platonischen Körper.
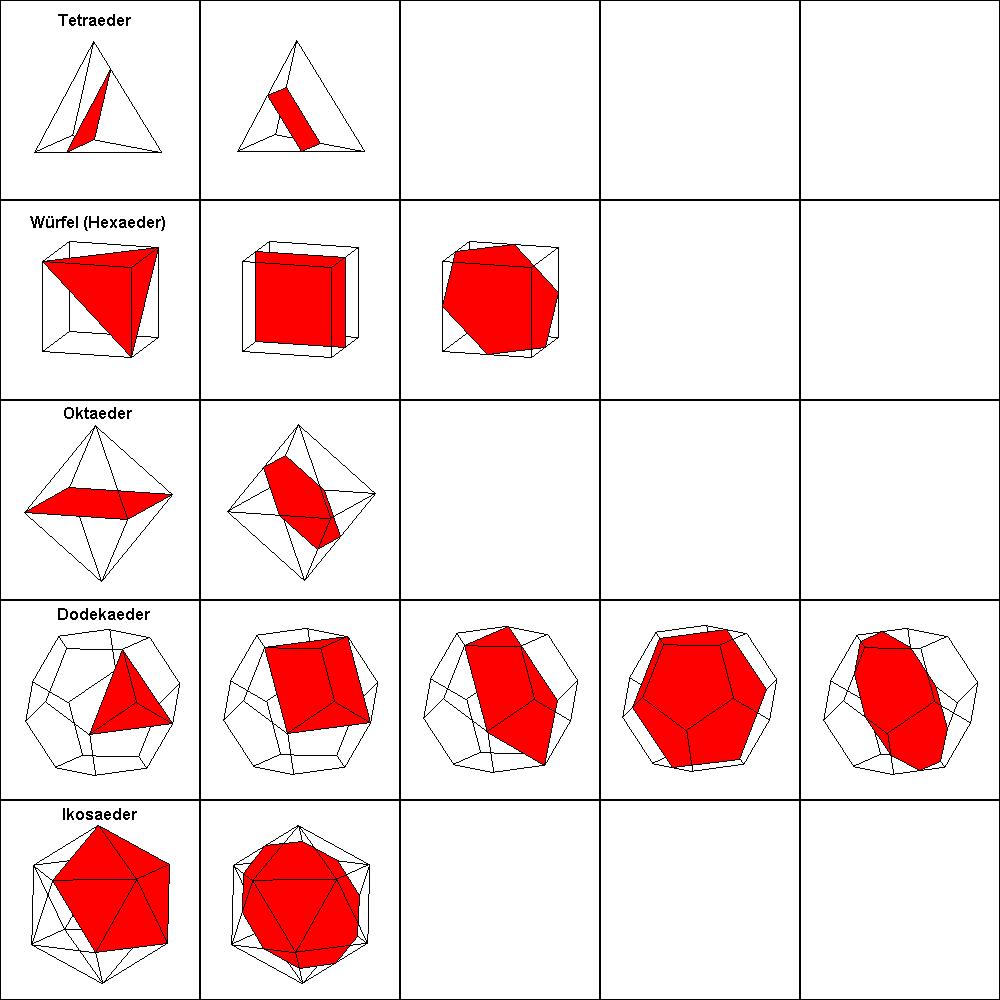
Bei platonischen Körpern werden aus den Schnitten durch die Seitenflächen der platonischen Körper die Seiten der Schnittflächen.
Beim Tetraeder können also höchstens Vierecke, beim Oktaeder höchstens Achtecke, beim Dodekaeder höchstens Zwölfecke und beim Ikosaeder
höchstens 20-Ecke als Schnittflächen entstehen. Außerdem liegen die Ecken der Schnittflächen auf den Kanten der platonischen Körper.
Um diese Kanten miteinander zu verbinden, benötigt man mindestens die gleiche Anzahl von Ecken auf den platonischen Körpern. Die Anzahl
der Ecken der Schnittflächen kann also höchstens gleich der Anzahl der Ecken der platonischen Körper sein. Durch diese weitere
Einschränkung ist die maximale Anzahl der Ecken der Schnittflächen beim Tetraeder 4, beim Oktaeder 6, beim Dodekaeder 12 und
beim Ikosaeder ebenfalls 12.
Weil eine Schnittfläche mindestens so viele Seiten haben muss, wie Flächen an einer Ecke des Würfels zusammenstoßen, sind die
Schnittflächen beim Tetraeder mindestens Dreiecke, beim Oktaeder mindestens Vierecke, beim Dodekaeder mindestens Dreiecke
und beim Ikosaeder mindestens Fünfecke.
Tetraeder:
Beim Tetraeder können nach den obigen Überlegungen nur Dreiecke und Vierecke als Schnittflächen entstehen. Schneidet man das Tetraeder
geeignet durch, kann man tatsächlich gleichseitige Dreiecke und Quadrate als Schnittflächen bekommen.
Oktaeder:
Beim Oktaeder sind nach den obigen Überlegungen Vierecke, Fünfecke und Sechsecke als Schnittflächen möglich.
Wie die Abbildung zeigt, kann man das Oktaeder so schneiden, dass Quadrate und regelmäßige Sechsecke entstehen.
Aus dem gleichen Grunde, der schon beim Würfelschnitt angegeben wurde, kann man auch hier keine regelmäßigen Fünfecke
als Schnittflächen erzeugen.
Dodekaeder:
Beim Dodekaeder sind als Schnittflächen alle Vielecke vom Dreieck bis zum Zehneck machbar. Hier gibt es die meisten regelmäßigen
Vielecke. Man kann durch Schneiden gleichseitige Dreiecke, Quadrate, regelmäßige Fünfecke, regelmäßige Sechsecke und
regelmäßige Zehnecke erzeugen. Aus dem gleichen Grunde, der schon beim Würfelschnitt angegeben wurde, sind keine regelmäßigen Siebenecke
und Neunecke möglich.
Ikosaeder:
Beim Ikosaeder sind als Schnittflächen alle Vielecke vom Fünfeck bis zum Zwölfeck machbar. Man kann durch Schneiden regelmäßige Fünfecke
und Zehnecke erzeugen. Aus dem gleichen Grunde, der schon beim Würfelschnitt angegeben wurde, sind keine regelmäßigen Elfecke möglich.
Copyright © Werner Brefeld (2005)