 |
Geodätische Kuppeln
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum,
Themenübersicht auf der Hauptseite:
Mathematik im Alltag, verblüffende Mathematik-Rätsel, Stochastik und Polyeder, irdisches und außerirdisches Leben
|
Was sind geodätische Kuppeln und wie erzeugt man sie?
Möchte man eine Kuppel möglichst kugelförmig aus ebenen Flächen zusammensetzen,
so sollte man Dreiecke verwenden, die möglichst gleichseitig sind und deren Ecken alle auf einer
Kugeloberfläche liegen. Solche Kuppeln besitzen also eine sogenannte Umkugel.
Mit exakt gleichseitigen Dreiecken kommt man nicht weit, da die Mathematik nur drei solcher Körper
ermöglicht. Befinden sich an jeder Ecke drei gleichseitige Dreiecke, ist der Körper ein
Tetraeder. Man wird hier kaum von einer annähernd kugelförmigen Gestalt reden
können. Ein Oktaeder hat vier Dreiecke an jeder Ecke und ist schon deutlich
"runder". Beim Ikosaeder mit seinen fünf gleichseitigen Dreiecken an jeder Ecke
hat man zum ersten Mal das Gefühl, mit einem annähernd kugelförmigen Körper zu tun zu haben. Leider ergeben
sechs gleichseitige Dreiecke an einer Ecke keinen Körper mehr, da die entsprechenden sechs Innenwinkel der
Dreiecke zusammen 360° ergeben. Man kann damit allerdings ein ebenes Parkett
herstellen. Ein solches Parkett lässt sich natürlich auch interpretieren als Oberfläche eines unendlich großen
kugelförmigen Körpers. Dieser "Körper" hat zwar eine ideale "Oberfläche", schießt aber wegen seiner
Unendlichkeit über das gesteckte Ziel hinaus.
Deshalb ist der Gedanke naheliegend, Ecken mit fünf und sechs Dreiecken möglichst regelmäßig zu
kombinieren. Die Ecken mit fünf Dreiecken hätten dabei für die Krümmung der Oberfläche zu sorgen.
Ihre regelmäßige Anordnung würde einen angenähert kugelförmigen Körper erzeugen, wenn man alle
Ecken auf einer Kugeloberfläche platziert. Allerdings geht das nicht mehr mit exakt gleichseitigen
Dreiecken. Aber dieses Verfahren führt tatsächlich zu den oben gesuchten Kuppeln. Sie heißen
geodätische Kuppeln und werden verwendet für Sternwarten, Planetarien, Radaranlagen, Ausstellungshallen,
Gewächshäuser usw.
Diese geodätischen Kuppeln unterliegen einer interessanten Randbedingung. Zunächst gilt der
Eulersche Polyedersatz, der eine Beziehung zwischen der Anzahl der Flächen (F), der Kanten (K)
und der Ecken (E) herstellt:
F + E – K = 2
Da wir nur Polyeder mit Dreiecksflächen betrachten, jedes Dreieck drei Kanten hat, sich die Kanten
aber mit jeweils einem Nachbardreieck teilen muss, gilt hier außerdem:
K = 3/2 · F
Oben eingesetzt:
F + E – 3/2 · F = 2
E = 1/2 · F + 2
Von jeder Fünferecke (E5) gehen 5 Kanten aus. Jeder Kante gehört aber gleichzeitig zu einer anderen
Ecke. Das gilt entsprechend für die Sechserecken (E6). Damit muss gelten:
5/2 · E5 + 6/2 · E6 = K = 3/2 · F
5 · E5 + 6 · (E – E5) = 3 · F
E5 = 6 · E – 3 · F
E5 = 3 · F + 12 – 3 · F
E5 = 12
Die geodätischen Kuppeln besitzen also immer genau 12 Fünferecken. Die gleichmäßigste Verteilung dieser
Fünferecken entsteht, wenn sie zueinander genau so angeordnet werden wie die 12 Fünferecken eines Ikosaeders,
das die einfachste geodätische Kuppel darstellt. Bei einem Umkugelradius von 1 Meter hat das Ikosaeder eine
Seitenlänge von 1,0514622 Meter und der Flächenwinkel zwischen zwei benachbarten Dreiecken beträgt 138,1897°.
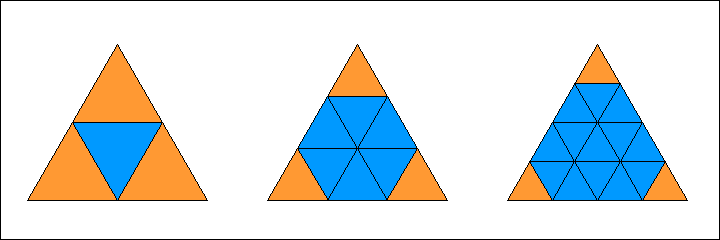
Der einfachste Weg (Verfahren 1), weitere geodätische Kuppeln zu konstruieren, besteht darin, das eben erwähnte Ikosaeder
als Ausgangskörper zu verwenden. Man teilt dabei die gleichseitigen Dreiecke des Ikosaeders in 4, 9, 16, usw. gleichseitige und gleich
große kleinere Dreiecke auf (siehe Abbildung). Man erhält also n2 kleinere Dreiecke, wobei n eine positive ganze Zahl ist.
Dabei entstehen auf den Seiten eines Ikosaeder-Dreiecks gleich viele und gleich lange Abschnitte. Außerdem bilden sich zusätzliche Sechserecken.
Diese projiziert man vom Ikosaeder-Mittelpunkt auf die Oberfläche der Umkugel. Die dabei neu entstehenden Dreiecke bilden in ihrer Gesamtheit
eine geodätische Kuppel. In je mehr kleinere Dreiecke die Ikosaeder-Dreiecke aufgeteilt werden, desto kugelförmiger wird die so erzeugte geodätische Kuppel.
|
Verfahren 2: Nach der Projektion sind die Dreiecke allerdings weder gleichseitig noch gleich groß. Dieses Problem
lässt sich grundsätzlich nicht vermeiden. Man kann aber gleichmäßigere Dreiecke bekommen als bei dem eben
beschriebenen einfachen Verfahren 1. Dazu versieht man die Seiten des Ikosaeder-Dreiecks so mit Markierungen,
dass nach Projektion dieser Markierungen auf die Umkugel die dazwischen liegenden geraden Teilstrecken gleich lang
werden. Die Markierungen auf den Ikosaeder-Seiten verbindet man dann in gleicher Weise wie beim einfachen Verfahren 1.
Allerdings schneiden sich dann nicht mehr jeweils 3 Strecken in einem Punkt wie oben, sondern sie bilden stattdessen
ein mehr oder weniger kleines gleichseitiges Dreieck. Die Mittelpunkte dieser Dreiecke werden ebenfalls markiert.
Alle Markierungen bilden dann nach Projektion auf die Umkugel die Sechserecken der neuen geodätischen Kuppel.
Allgemein besitzen diese geodätischen Kuppeln F = 20 · n2 Dreiecke, wobei n eine ganze Zahl größer Null ist.
|
|
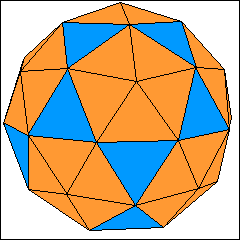
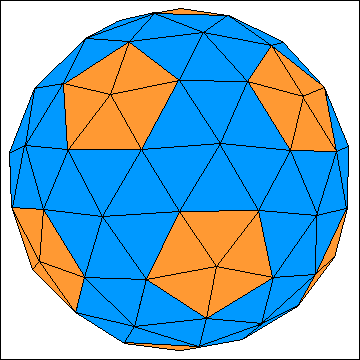
Die beiden Abbildungen zeigen die einfachsten geodätischen Kuppeln, die man aus einem Ikosaeder konstruieren kann.
Sie besitzen 80 bzw. 180 Dreiecke auf ihrer Oberfläche.
Die geodätische Kuppel mit 80 Dreiecken besitzt 20 gleichseitige und 60 gleichschenkliche Dreiecke. Bei einem Umkugelradius
von 1 Meter haben die Seiten dieser Kuppel die beiden unterschiedlichen Längen von 0,546533 Meter (Schenkel) und 0,618034 Meter.
Die Kuppel besitzt ebenfalls zwei unterschiedliche Flächenwinkel mit Werten von 157,5411° (Winkel zwischen zwei benachbarten
gleichschenkligen Dreiecken) und 161,9709°.
Die geodätische Kuppel mit 180 Dreiecken kann man noch nach einem weiteren Verfahren herstellen. Dazu nimmt man
das abgestumpfte Ikosaeder als Ausgangskörper und unterteilt die 20 Sechsecke in 6 gleichseitige Dreiecke und
die 12 Fünfecke in 5 gleichschenklige Dreiecke. Anschließend projiziert man die neu entstandenen Sechserecken
und Fünferecken vom Mittelpunkt des abgestumpften Ikosaeders auf die Oberfläche der Umkugel. Im Ergebnis ist
dieses Verfahren identisch mit dem Verfahren 1.
Für die geodätische Kuppel mit 320 Dreiecken gibt es ebenfalls noch ein weiteres Verfahren. Dazu teilt man die Ikosaeder-Dreiecke zuerst
wie oben beschrieben in 4 kleinere Dreiecke und projiziert die entstehenden Sechserecken auf die Umkugel. Die dabei neu entstehenden Dreiecke
teilt man wieder in 4 kleinere Dreiecke und projiziert die entstehenden Sechserecken wieder auf die Umkugel. Mit diesem zweistufigen
Verfahren erhält man ein sehr ähnliches Ergebnis wie beim Verfahren 2.
|
Die folgende Tabelle stellt Eigenschaften solcher Kuppeln mit bis zu 2000 Dreiecken zusammen
(Anordnung und Länge der einzelnen Kanten errechnet man am besten mit einem Computer-Programm.):
| Abstand der | Anzahl der | Anzahl | Anzahl | Anzahl | Anzahl der | Anzahl der |
| Fünferecken | Dreiecke pro | der | der | der | unterschiedlichen | unterschiedlichen |
| in Seitenlängen | Ausgangs- | Dreiecke | Ecken | Kanten | Dreiecke * | Kantenlängen |
| der Dreiecke | dreieck | | | | Verfahren 1 (2) | Verfahren 1 (2) |
| | | | | | |
| 1 (Ikosaeder) | 1 | 20 | 12 | 30 | 1 (1) | 1 (1) |
| 2 (Tetra-Ikosaeder) | 4 | 80 | 42 | 120 | 2 (2) | 2 (2) |
| 3 | 9 | 180 | 92 | 270 | 2 (3) | 3 (3) |
| 4 | 16 | 320 | 162 | 480 | 6 (6) | 6 (5) |
| 5 | 25 | 500 | 252 | 750 | 9 (9) | 9 (7) |
| 6 | 36 | 720 | 362 | 1080 | 8 (12) | 9 (10) |
| 7 | 49 | 980 | 492 | 1470 | 17 (17) | 16 (13) |
| 8 | 64 | 1280 | 642 | 1920 | 22 (22) | 20 (17) |
| 9 | 81 | 1620 | 812 | 2430 | 18 (27) | 20 (21) |
| 10 | 100 | 2000 | 1002 | 3000 | 34 (34) | 30 (26) |
* Spiegelsymmetrische Dreiecke gelten als unterschiedlich.
Aus den Kuppeln mit n = 2, 4, 6, 8 und 10 lassen sich gut Halbkuppeln konstruieren.
Diese Halbkuppeln haben dann jeweils die Hälfte der Dreiecke und 65, 250, 555, 980 und 1525 Kanten.
Die unteren Kanten dieser Halbkuppeln liegen sogar exakt in einer Ebene, wenn man sie nach Verfahren 1 konstruiert.
Dazu müssen aber an der Spitze der Halbkuppel 5 Dreiecke zusammenstoßen. Der Grund dafür ist, dass ein in der Mitte
durchgeschnittenes in gleicher Weise orientiertes Ikosaeder als Schnittfläche
ein ebenes regelmäßiges Zehneck besitzt.
Berechnungen der Kantenlängen einer geodätischen Kuppel mit 80 Dreiecken:
Für diese Kuppel mit ihren 60 gleichschenkligen und 20 gleichseitigen Dreiecken kann man die beiden verschiedenen Seitenlängen der Dreiecke
noch relativ leicht berechnen.Angenommen, der Umkugelradius betrage ru = 1 Meter. In die entsprechende Umkugel platziert man ein Ikosaeder
und berechnet die Seitenlänge s seiner Dreiecke. Zwischen ru und s gilt die Beziehung:
ru = s/4 · √(10 + 2·√5)
Nach s umgeformt ergibt sich:
s = ru /5 · √(50 – 10·√5) = 1,051462 m
Dann werden die Mittelpunkte der Ikosaederkanten auf die Umkugel projiziert. Diese neuen Punkte bestimmen zusammen mit den Ecken des Ikoaseders
die Länge a der Schenkel der gleichschenkligen Dreiecke der Kuppel. Es gilt nach zweimaligem Anwenden des Pythagoras-Satzes:
a = √((s/2)2 + (ru – √(ru2 – (s/2)2))2) = 0,546533 m
Zur Bestimmung der Seitenlänge b der gleichseitigen Dreiecke kann man auf einen Trick zurückgreifen. Man stellt sich jeweils 5 gleichschenklige Dreiecke,
die an einer Ecke zusammenstoßen, als ein ebenes regelmäßiges Fünfeck vor. Die Ecken dieses Fünfecks liegen ja immer noch auf der obigen Umkugel.
Alle Fünfecke zusammen ergeben mit den gleichseitigen Dreiecken ein sogenanntes Ikosidodekaeder.
Zwischen dem Umkugelradius r und den Kantenlängen b des Ikosidodekaeders gilt die einfache Beziehung:
ru = b/2 · (1 + √5)
Nach b umgeformt ergibt sich schließlich:
b = ru /2 · (√5 – 1) = 0,618034 m
Die 20 gleichseitigen Dreiecke haben also Seitenlängen von 0,618034 Meter und
die 60 gleichschenkligen Dreiecke von einmal 0,618034 Meter und zweimal 0,546533 Meter.
Berechnungen der Flächenwinkel einer geodätischen Kuppel mit 80 Dreiecken:
Für die Seitenlängen der Dreiecke der Kuppel werden wieder die oben verwendeten Bezeichnungen a und b,
für die Kantenlänge des zugrunde liegenden Ikosaeders die Bezeichnung s und für den Umkugelradius die Bezeichnung ru verwendet.
Nach dem Satz des Pythagoras ergibt sich dann für die Höhe h1 eines gleichseitigen Dreiecks:
h1 = 0,5 · √3 · b = 0,535233 m
Höhe h2 eines gleichschenkligen Dreiecks (Satz des Pythagoras):
h2 = √(a2 – (b/2)2) = 0,450785 m
Winkel φ zwischen der Strecke von der Ecke eines gleichseitigen Dreiecks bis zum Umkugelmittelpunkt
und der Strecke vom Umkugelmittelpunkt bis zur Ecke eines benachbarten gleichschenkligen Dreiecks (gegenüberliegende Ecke):
φ = 90° – arcsin((s/2)/ru) = 58,2825°
Abstand e der Ecken eines gleichseitigen und eines benachbarten gleichschenkligen Dreiecks (gegenüberliegende Ecken):
e = 2 · sin(φ/2) · ru = 0,973929 m
Flächenwinkel α zwischen einem gleichseitigen und einem benachbarten gleichschenkligen Dreieck (Cosinus-Satz):
α = arccos((h12 + h22 – e2) / (2 * h1 · h2)) = 161,9709°
Abstand f der Ecken zweier benachbarter gleichschenkliger Dreiecke (gegenüberliegende Ecken):
f = 2 · b · sin(108° / 2) = 1
Höhe ha des gleichschenkligen Dreiecks, die das Dreieck nicht symmetrisch teilt (Heron'sche Formel):
ha = 2 · √(x · (x – a)2 · (x – b)) / a = 0,509759 m
mit x = (2 · a + b) / 2 = 0,855550 m
Flächenwinkel β zwischen zwei benachbarten gleichschenkligen Dreiecken:
β = 2 · arcsin((f/2) / ha) = 157,5411°
Ergänzung: Berechnung des Flächenwinkels des zugrunde liegenden Ikosaeders:
Der Abstand rs einer Seitenmitte zum Mittelpunkt des Ikosaeders beträgt (Satz des Pythagoras):
rs = Wurzel(ru2 – (s/2)2) = 0,850651 m
Höhe h eines gleichseitigen Dreiecks (Satz des Pythagoras):
h = 0,5 · √3 · s = 0,910593 m
Winkel δ im Dreieck mit den Seitenlängen rs, h und ru gegenüber der Seite ru (Cosinus-Satz):
δ = arccos((rs2 + h2 – ru2) / (2 · rs · h)) = 69,0948°
Flächenwinkel γ zwischen zwei benachbarten Dreiecken:
γ = 2 · δ = 138,1897°
|
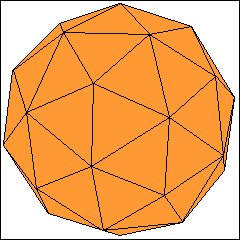
Eine weitere Möglichkeit zur Konstruktion geodätischer Kuppeln ist die Nutzung des Dodekaeders
als Ausgangskörper. Dazu verbindet man die Ecken der 12 Fünfecke mit dem Mittelpunkt des jeweiligen Fünfecks und erhält so die 12 Fünferecken,
die man wieder auf die Umkugel übertragen muss. Aus dieser eindeutig definierten geodätischen Kuppel mit 60 gleichschenkligen Dreiecken kann man
wieder eine Serie von geodätischen Kuppeln erzeugen, indem man - wie oben - die Dreiecke nach einem der beiden Verfahren weiter unterteilt.
Allerdings muss man dabei beachten, dass man die Schritte für die unterschiedlich langen Kanten der gleichschenkligen Dreiecke getrennt durchführt.
Was die geodätische Kuppel mit 60 Dreiecken angeht, so sollte man sie nicht mit dem sehr ähnlichen Pentakisdodekaeder verwechseln, der als
catalanischer Körper dual zum abgestumpften Ikosaeder ist. Der Pentakisdodekaeder besitzt nämlich keine Umkugel.
Diese vom Dodekaeder abgeleiteten geodätischen Kuppeln haben F = 60 · n2 Dreiecke, wobei n eine ganze Zahl größer Null ist.
|
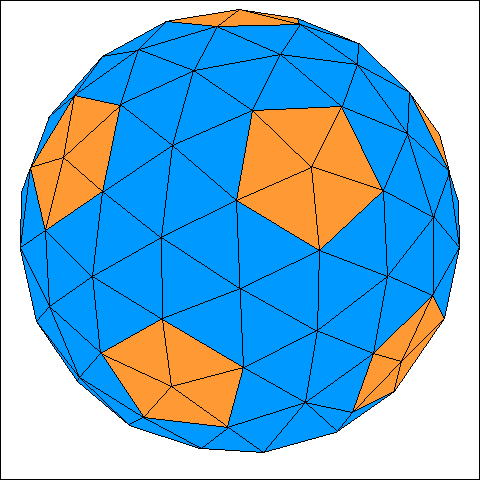
|
Die beiden Abbildungen zeigen die einfachsten geodätischen Kuppeln, die man aus einem Dodekaeder konstruieren kann.
Sie besitzen 60 bzw. 240 Dreiecke auf ihrer Oberfläche.
Bei der geodätischen Kuppel mit 60 Dreiecken sind alle Dreiecke gleichschenklig. Bei einem Umkugelradius von 1 Meter haben die Seiten dieser Kuppel
die beiden unterschiedlichen Längen von 0,640852 Meter (Schenkel) und 0,713644 Meter. Die Kuppel besitzt ebenfalls zwei unterschiedliche Flächenwinkel
mit Werten von 153,7896° (Winkel zwischen den über ihre Schenkel benachbarten Dreiecken) und 161,9460°.
|
Die folgende Tabelle stellt wieder Eigenschaften solcher Kuppeln mit bis zu 2000 Dreiecken zusammen
(Anordnung und Länge der einzelnen Kanten errechnet man am besten mit einem Computer-Programm.):
| Abstand der | Anzahl der | Anzahl | Anzahl | Anzahl | Anzahl der | Anzahl der |
| Fünferecken | Dreiecke pro | der | der | der | unterschiedlichen | unterschiedlichen |
| in Seitenhöhen | Ausgangs- | Dreiecke | Ecken | Kanten | Dreiecke * | Kantenlängen |
| der Dreiecke | dreieck | | | | Verfahren 1 (2) | Verfahren 1 (2) |
| | | | | | | |
| 2 (Penta-Dodekaeder) | 1 | 60 | 32 | 90 | 1 (1) | 2 (2) |
| 4 | 4 | 240 | 122 | 360 | 4 (4) | 4 (4) |
| 6 | 9 | 540 | 272 | 810 | 9 (9) | 9 (7) |
| 8 | 16 | 960 | 482 | 1440 | 16 (16) | 14 (12) |
| 10 | 25 | 1500 | 752 | 2250 | 25 (25) | 22 (18) |
* Spiegelsymmetrische Dreiecke gelten als unterschiedlich.
Berechnungen der Kantenlängen einer geodätischen Kuppel mit 60 Dreiecken:
Für diese Kuppel mit ihren 60 gleichschenkligen Dreiecken kann man die beiden verschiedenen Seitenlängen der Dreiecke noch relativ leicht berechnen.
Angenommen, der Umkugelradius betrage ru = 1 Meter. In die entsprechende Umkugel platziert man ein Dodekaeder und zerlegt jedes Fünfeck des Dodekaeders
in 5 gleichschenklige Dreiecke. Zwischen ru und der Seite a eines Fünfecks gilt die Beziehung:
ru = (a/4) · √3 · (1 + √5)
Damit gilt für die Seite a eines Fünfecks:
a = 4·ru / (√3 · (1 + √5)) = 0,713644 m
Diese Seite ist identisch mit einer Seite der Dreiecke der Kuppel. Man muss jetzt noch die Länge der Schenkel der beiden anderen Seiten bestimmen.
Die Länge rf von einer Ecke eines Fünfecks bis zum Mittelpunkt des Fünfecks beträgt:
rf = (a/2) / sin36° = 0,607062 m
Das wäre schon das Ergebnis, wenn der Mittelpunkt des Fünfecks nicht auf der Inkugel des Dodekaeders, sondern auf der Umkugel läge.
Der Inkugelradius ri beträgt aber nur:
ri = ru · √(75 + 30·√5) / 15 = 0,794654 Meter.
Man muss den Mittelpunkt des Fünfecks also um ru – ri anheben, damit die entsprechenden Dreiecke mit ihren Ecken auch auf der Umkugel liegen.
Nach dem Satz des Pythagoras ergibt sich deshalb für die Schenkel b der gleichschenkligen Dreiecke die Länge:
b = √((ru – ri)2 + rf2) = 0,640852 m
Die 60 gleichschenkligen Dreiecke haben also Seitenlängen von einmal 0,713644 Meter und zweimal 0,640852 Meter.
Wenn man bei der Berechnung die Formel b = 3/38 · a · (9 + √5) verwendet, dann bekommt man die Schenkellänge b für die 60 gleichschenkligen Dreiecke
des Pentakisdodekaeders. Sie beträgt 0,633044 Meter, im Gegensatz zu den 0,640852 Meter für die geodätische Kuppel mit 60 Dreiecken.
Das Pentakisdodekaeder ist ein catalanischer Körper und hat im Gegensatz zur geodätischen Kuppel keine Umkugel, dafür aber eine Inkugel.
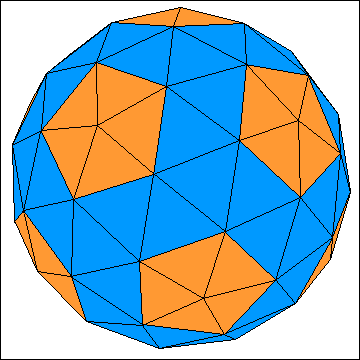
|
Die beiden erwähnten Serien sind die einzigen, bei denen die Körper Symmetrieebenen besitzen. Es gibt zusätzlich noch
unendlich viele Serien von "verdrehten" geodätischen Kuppeln. Die einfachste dieser Serien entsteht, wenn man das
abgeschrägte Dodekaeder als Ausgangskörper nimmt, die 80 Dreiecke zunächst nicht ändert
und mit den 12 Fünfecken wie beim Dodekaeder verfährt. Die Abbildung zeigt die einfachste geodätische Kuppel dieser
Serie. Sie besitzt 140 Dreiecke.
|
Und hier kommt die Tabelle mit den Eigenschaften der einfachsten Serie der "verdrehten" geodätischen Kuppeln mit bis zu 2000 Dreiecken:
| Abstand der | Anzahl der | Anzahl | Anzahl | Anzahl |
| Fünferecken | Dreiecke pro | der | der | der |
| in Seitenlängen | Ausgangs- | Dreiecke | Ecken | Kanten |
| der Dreiecke | dreieck | | | |
| | | | | |
| ca. 2,5 | 1 | 140 | 72 | 210 |
| ca. 5 | 4 | 560 | 282 | 840 |
| ca. 7,5 | 9 | 1260 | 632 | 1890 |
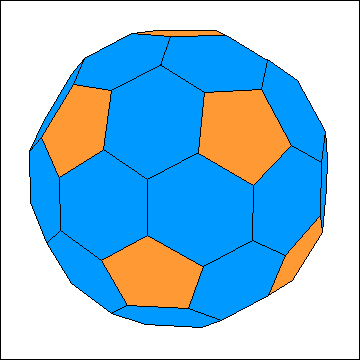
|
Interessant sind auch die zu den geodätischen Kuppeln dualen Polyeder. Sie besitzen neben 12 regelmäßigen Fünfecken nur Sechsecke auf ihrer
Oberfläche und werden ebenfalls zum Kuppelbau verwendet. Man erhält sie, indem man durch die Ecken einer geodätischen Kuppel die Tangentialebenen
an die Umkugel dieser geodätischen Kuppel legt. Die Schnittgeraden der Tangentialebenen durch benachbarte Ecken bilden dann die Seiten
der dualen Kuppel.
Die einfachste derartige Kuppel ist das Dodekaeder (12 Fünfecke, keine Sechsecke). Es ist dual zum Ikosaeder und
die Ausgangskuppel einer Serie, die F = (10 · n2 + 2) Flächen (12, 42, 92, 162, 252, 362, 492, 642, 812, 1002, ...) besitzt.
Die Abbildungen zeigen die beiden nächsten Kuppeln dieser Serie, nämlich den "großen Fußball" mit 42 Flächen (12 Fünfecke und 30 Sechsecke)
und die duale Kuppel mit 92 Flächen (12 Fünfecke und 80 Sechsecke). Den "großen Fußball" kann man durch das Abstumpfen der Fünferecken
eines Rhombentriakontaeders (dual-archimedischer oder catalanischer Körper) herstellen und eine geodätische Kuppel mit 60 Dreiecken kann man
durch Abstumpfen in die duale Kuppel mit 92 Flächen umwandeln.
|
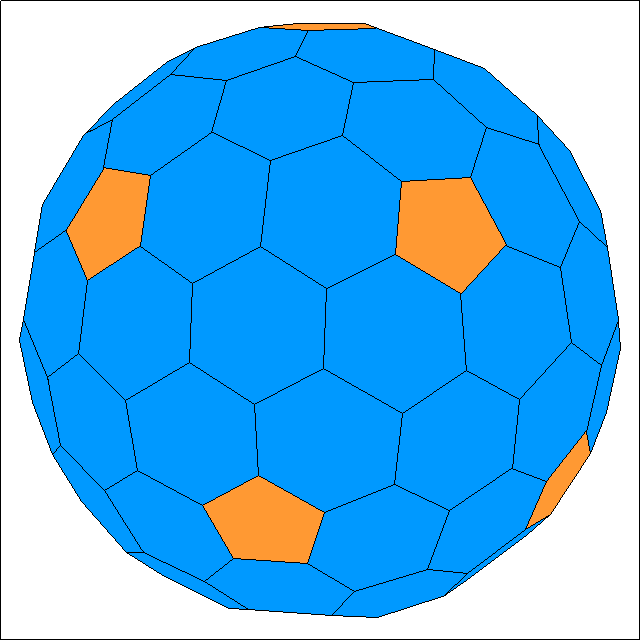
|
Eine zweite Serie hat F = (30 · n2 + 2) Flächen (32, 122, 272, 482, 752, ...) und ist dual zu den geodätischen Kuppeln mit
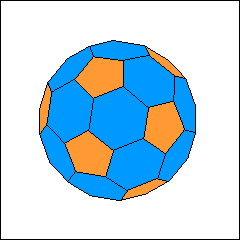
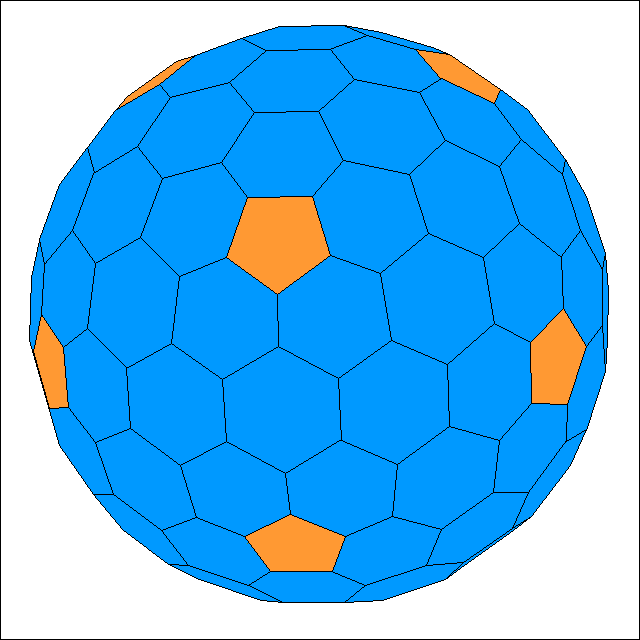
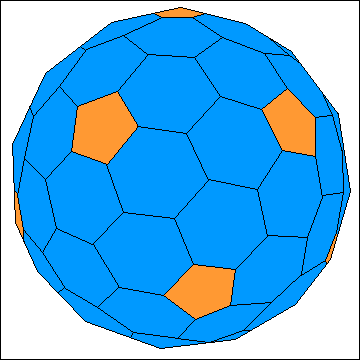
60, 240, 540, ... Dreiecken. Sie beginnt mit dem abgestumpften Ikosaeder (Fußballkörper), das 32 Flächen (12 Fünfecke und 20 Sechsecke) besitzt.
Wie der Name schon sagt, erhält man diesen Körper durch das Abstumpfen eines Ikosaeders. Danach folgt eine duale Kuppel mit 122 Flächen
(12 Fünfecke und 110 Sechsecke) auf der Oberfläche. Ihn kann man durch das Abstumpfen der geodätischen Kuppel herstellen, die 80 Dreiecke besitzt.
Die Abbildungen zeigen diese beiden Kuppeln mit den 32 bzw. 122 Flächen.
|
|
Schließlich zeigt die letzte Abbildung die duale Kuppel zur einfachsten "verdrehten" geodätischen Kuppel. Sie besitzt 72 Flächen (12 Fünfecke
und 60 Sechsecke) auf der Oberfläche. Man kann sie durch Abstumpfen der Fünferecken eines Pentagonhexakontaeders
(dual-archimedischer oder catalanischer Körper) herstellen.
|
Die oben erwähnten platonischen Körper und archimedischen Körper findet man
auf der Web-Seite über reguläre und halbreguläre Polyeder.
Links zum Thema:
Wikipedia: Archimedische Körper
Wikipedia: Catalanische Körper
Jürgen Köller: Deltaeder
Jürgen Köller: Johnson-Körper
Jürgen Köller: Die Kuppeln unter den Johnson-Körpern
Arndt Brünner: Platonische und Archimedische Körper
Referenz: Reguläre und halbreguläre Polyeder (Tiberiu Roman, Deutsch Taschenbücher, Band 56)
Copyright © Werner Brefeld (2006)











