 |
Mathematik - Hintergründe im täglichen Leben (Werner Brefeld)
* * * gemeinnützige Website seit 2005 * * *
(Hauptthema: Nützlichkeit und Hintergründe der Mathematik im täglichen Leben)
Weitere Themen:
Verblüffende Mathematik-Rätsel, Stochastik, Lotto, Kniffel und Polyeder, irdisches und außerirdisches Leben, Raumfahrt
Fragen und Bemerkungen gerne an: werner.brefeld@web.de, Adresse: siehe Impressum
Siehe auch mein Rowohlt-Taschenbuch
"Voll auf die 12 - Besser durchs Leben mit Mathematik"
|
Mathematik im Alltag
Mathematik im Alltag (nützliche Beispiele)
Wie viel Mathematik sollte jeder können, damit er im Alltag keine Nachteile hat? Welches sind die
wichtigsten Mathematikaufgaben, die man zur Bewältigung des Alltags beherrschen sollte?
Teilbarkeit hochzusammengesetzter Zahlen
Welche Zahlen haben eine hohe Teilbarkeit, eignen sich also am besten, um etwas zu unterteilen?
Warum haben Tag und Nacht jeweils 12 Stunden, eine Stunde 60 Minuten, eine Minute 60 Sekunden und der Vollkreis 360°?
Zahlensysteme, kleines Einmaleins und Teilbarkeitsregeln
Welches sind die besten Zahlensysteme für den Alltag? Warum hat unser Zahlensystem 10 Ziffern?
Geldsysteme und Zahlensysteme
Welche Zahlen sollten auf Geldmünzen und Geldscheinen stehen? Warum gibt es 1€- und 2€-Stücke,
5€-, 10€-, 20€-, 50€-Scheine?
DIN-Papier und Goldener Schnitt
Welches sind die günstigsten Seitenverhältnisse für rechteckige Papierblätter und Briefumschläge?
Warum ist das Verhältnis der Seiten eines DIN-Blattes gleich Wurzel aus 2?
Tonsysteme, Zwölftonsystem, Quinte, Quarte und Terz
Welches sind die besten Tonsysteme in der Musik?
Warum besitzt das Klavier 12 Tasten für jede Oktave?
Zweiklang, Konsonanz, Dissonanz, Oktave, Quinte, Quarte und Terz
Welches sind die konsonanten Zweiklänge (Intervalle) in der Musik?
Warum klingt die Quinte sehr konsonant (wohlklingend), die kleine Sekunde dagegen sehr dissonant (schräg)?
Fußball, Platonische Körper und Archimedische Körper
Welcher platonische Körper oder archimedische Körper eignet sich am besten als Fußball?
Warum besteht der Fußball oft aus 20 regelmäßigen Sechsecken und 12 regelmäßigen
Fünfecken?
Lottosysteme, Kombinatorik und Wahrscheinlichkeitsrechnung
Welches sind die besten Lottosysteme? Warum werden beim Lotto 6 aus 49 Kugeln gezogen?
Wahlverfahren und die Uneindeutigkeit der Wahl eines Kandidaten
Welches sind sinnvolle Wahlverfahren, um unter drei Kandidaten einen auszuwählen?
Warum können Wahlverfahren zu unterschiedlichen Gewinnern führen?
Wahlverfahren und die Uneindeutigkeit der Sitzverteilung im Parlament
Welches sind sinnvolle Wahlverfahren für eine Parlamentswahl, um die Sitzverteilung für die Abgeordneten zu bestimmen?
Warum können Wahlverfahren zu unterschiedlichen Mandatsverteilungen führen?
Gregorianischer Kalender und die Regel für die Schaltjahre
Welche Regel eignet sich am besten zum Festlegen der Schaltjahre? Warum verwendet die
geltende Schaltjahrregel Zeitintervalle von 4, 100 und 400 Jahren?
Verblüffende Mathematik-Rätsel
Verblüffend,
weil es überhaupt eine Lösung gibt, weil es nur eine Lösung gibt,
weil es eine überraschende Lösung gibt, weil es neben einer einfachen
noch weitere unerwartete Lösungen gibt, weil das Ergebnis so klein oder so groß ist
oder weil die aufgestellte Behauptung überhaupt gilt.
1. Abdeckung einer Kreisscheibe
Gegeben sei eine Kreisscheibe. Wie viele Kreisscheiben mit dem halben
Durchmesser braucht man mindestens, um die große Scheibe vollständig abzudecken?
2. Regelmäßiges Vieleck und Zerschneiden
Welche Möglichkeiten gibt es, ein beliebiges regelmäßiges Vieleck in mehrere
regelmäßige Vielecke mit der gleichen Seitenlänge zu zerschneiden?
3. Räuber, Beute und Stammbrüche
Drei Räuber wollen ihre Beute aufteilen. Der zweite Räuber soll weniger als der erste und der dritte
weniger als der zweite bekommen. Ihre Anteile sollen aber Stammbrüche der gesamten Beute sein,
also 1/2, 1/3, 1/4, usw.. Wie viel bekommt jeder?
4. Matherätsel mit Grundrechenarten
In einer Rechenaufgabe sollen nur die Zahlen 1,3,4 und 6 vorkommen, und zwar auch jeweils nur genau
einmal. Zum Verknüpfen der Zahlen sind nur die 4 Grundrechenarten erlaubt. Klammern dürfen beliebig
gesetzt werden. Das Ergebnis soll 24 betragen. Wie lautet die Aufgabe?
Beispiele:
3 · 6 + 4 – 1 = 21
3 / (1 / 6) + 4 = 22
3 + 4 · (6 – 1) = 23
(6 + 1) · 4 – 3 = 25
4 · 6 + 3 – 1 = 26
(6 + 4 – 1) · 3 = 27
5. Neunstellige Zahl und Teilbarkeit
Es gibt nur eine neunstellige Zahl, bei der jede Ziffer von 1 bis 9 genau einmal vorkommt,
und bei der die erste Ziffer durch 1, die Zahl aus den ersten beiden Ziffern durch 2, die Zahl aus den
ersten 3 Ziffern durch 3, ... und die ganze Zahl durch 9 ohne Rest teilbar ist. Welche Zahl ist das?
Beispiel: 123654789
1 ist durch 1 teilbar.
12 ist durch 2 teilbar.
123 ist durch 3 teilbar.
1236 ist durch 4 teilbar.
12365 ist durch 5 teilbar.
123654 ist durch 6 teilbar.
1236547 ist nicht durch 7 teilbar! 123654789 ist also keine Lösung!
6. Neunstellige Zahl und kleines Einmaleins
Es gibt nur eine neunstellige Zahl, bei der jede Ziffer von 1 bis 9 genau einmal vorkommt,
und bei der die Zahl aus ihrer ersten und zweiten Ziffer, die Zahl aus ihrer zweiten und dritten Ziffer, ... und
die Zahl aus ihrer achten und neunten Ziffer alle ein Ergebnis des kleinen Einmaleins darstellen.
Welche Zahl ist das?
Beispiel: 124563789
12 = 3 · 4
24 = 4 · 6
45 = 5 · 9
56 = 7 · 8
63 = 7 · 9
37 ist kein Ergebnis des kleinen Einmaleins! 124563789 ist also keine Lösung!
7. Primzahlen, Teilbarkeit und die Zahl 24
Man nehme eine Primzahl größer als 3, multipliziere sie mit sich selbst und ziehe 1 davon ab.
Warum ist das Ergebnis immer ohne Rest durch 24 teilbar?
Beispiele:
5 · 5 – 1 = 24 = 1 · 24
7 · 7 – 1 = 48 = 2 · 24
11 · 11 – 1 = 120 = 5 · 24
13 · 13 – 1 = 168 = 7 · 24
17 · 17 – 1 = 288 = 12 · 24
19 · 19 – 1 = 360 = 15 · 24
8. Primzahlen, Teilbarkeit und die Zahl 240
Man nehme eine Primzahl größer als 5, multipliziere sie mit sich selbst, das Ergebnis auch, und
ziehe dann 1 davon ab. Warum ist das Endergebnis immer ohne Rest durch 240 teilbar?
9. Imaginäre Zahlen und imaginäre Einheit
Was ist das Ergebnis von Wurzel aus ii, wenn i die imaginäre Einheit ist?
10. Welche mathematische Funktion ist gleich ihrer dritten Ableitung?
Die Funktion y = ex ist identisch mit ihrer 1. Ableitung. Die Funktionen y = e–x
und y = –e–x reproduzieren sich erst mit der 2. Ableitung und die Funktionen y = sin(x), y = cos(x),
y = –sin(x) und y = –cos(x) erst mit der 4. Ableitung. Gibt es Funktionen, die erst wieder mit ihrer
3. Ableitung identisch sind und wie lautet ein Beispiel?
11. Zerteilen einer Schokolade
Eine Tafel Schokolade bestehe beispielsweise aus 4 · 6 = 24 Stücken. Will man sie völlig in die
24 Einzelstücke zerteilen, so kann man verschieden vorgehen. Zum Beispiel kann man zunächst durch fünf
Brechungen 6 Schokoladenstreifen aus je 4 Stücken erzeugen. Um die Einzelstücke zu erhalten, muss man dann
jeden dieser Streifen dreimal brechen. Insgesamt benötigt man also 5 + 3 · 6 = 23 Brechungen.
Ist es möglich (ohne Schokoladenteile übereinander zu legen), durch geschickteres Brechen mit weniger als
23 Brechungen auszukommen?
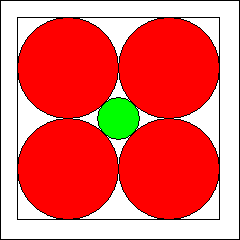
12. Hyperkugel im Hyperwürfel
In einem Quadrat mit der Seitenlänge 4 befindet sich in jeder Ecke ein Kreis mit dem Radius 1.
Im Zentrum des Quadrates ist ein weiterer Kreis, der die anderen vier berührt. Analog befände sich im
dreidimensionalen Fall im Zentrum eines Würfels der Kantenlänge 4 eine Kugel, die acht in den Ecken des
Würfels platzierte Kugeln mit Radius 1 berühren würde. In welcher Dimension wird die zentrale Hyperkugel
so groß, dass sie alle Seitenflächen des Hyperwürfels berührt?
13. Gespanntes Seil um den Äquator der Erde
Ein Seil wird straff um den Äquator gespannt und anschließend um 1 Meter verlängert.
Wie hoch kann man das Seil nun an einer Stelle ziehen, bis es wieder straff wird, wenn man für den
Radius der Erde eine Länge von 6378 km annimmt?

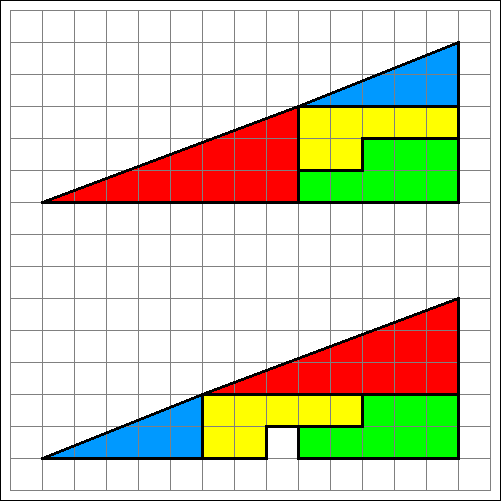
14. Dreieck aus Puzzleteilen mit Lücke?
Werden in der abgebildeten Figur die vier Puzzleteile anders angeordnet, entsteht plötzlich
eine Lücke. Ist die Gesamtfläche etwa kleiner geworden?
15. Professor Suzuki und seine drei Kinder
Professor Suzuki und Professor Baba begegnen sich in der Mensa der Waseda-Universität.
Suzuki: "Guten Abend, mein Bester. Wie geht es Ihnen?"
Baba: "Hervorragend, danke. Und Ihnen?"
Suzuki: "Sehr gut. Sie wissen, dass ich inzwischen drei Kinder habe ..."
Baba: "Wirklich? Wie alt sind sie denn?"
Suzuki: "Nun, Sie als guter Mathematiker und Logiker dürften es rasch herausbekommen.
Das Produkt ihrer Lebensalter ist 36, und die Summe ihrer Lebensalter ist identisch
mit der Nummer des Hauses, das Sie in Osaka bewohnten."
Baba (nach einer Pause): "Diese Informationen reichen mir nicht."
Suzuki: "Sie haben recht. Also, das älteste Kind hat blaue Augen."
Baba: "Aha, jetzt weiß ich, wie alt sie sind."
Wie alt sind die Kinder im Einzelnen?
16. Der Bischof und die drei Kirchenbesucher
Ein Pfarrer sagt zum Organisten: "Heute waren nur drei Leute in der Kirche."
Organist: "Wie alt waren denn die drei?"
Pfarrer: "Also wenn Du die jeweiligen Alter miteinander multiplizierst, dann ergibt das 2450.
Zusammen genommen sind sie so alt wie Du."
Organist: "Hmm, also mit diesen Informationen kann ich das ja wohl noch nicht lösen!"
Pfarrer: "Ach ja, ich muss noch erwähnen, dass alle drei jünger waren als unser Bischof!"
Organist: "Aha, jetzt hab ich die Lösung!"
Wie alt ist der Bischof?
17. Geburtstag am gleichen Tag
Wie viele Schüler müssen mindestens in einer Klasse sein, damit die Wahrscheinlichkeit,
dass mindestens zwei Schüler am gleichen Tag Geburtstag haben, größer ist, als dass alle an
unterschiedlichen Tagen Geburtstag haben?
18. Der Tangens der drei Innenwinkel im Dreieck
In einem Dreieck sei der Tangens der drei Innenwinkel jeweils eine positive ganze Zahl.
Wie lautet die einzige Lösung?
19. Würfelschnitt und regelmäßige Vielecke
Welche regelmäßigen Vielecke können entstehen, wenn man einen Würfel einmal durchschneidet?
20. Blattlaus und Mammutbaum
Eine Blattlaus sitzt am Fuße eines 15m hohen Mammutbaumes. Sie krabbelt zu Beginn des
Jahres 2cm am Stamm nach oben. Den Rest des Jahres wächst der Mammutbaum entlang seiner gesamten Länge
gleichmäßig um 4cm. Dieser Vorgang wiederholt sich jedes Jahr: Die Blattlaus krabbelt 2cm weiter nach oben,
der Baum wächst anschließend um 4cm. Erreicht die Blattlaus auf diese Weise jemals die Spitze des Baumes?
Wenn ja, wie viele Jahre braucht sie und wie hoch ist der Baum dann?
21. Goldkette
Eine offene Goldkette besteht aus 63 Gliedern. Durch Aufbiegen von möglichst wenig Gliedern
soll die Goldkette so in Teilketten zerlegt werden, dass man jede beliebige Anzahl von Gliedern
zusammenlegen kann. Ein aufgebogenes Glied zählt als Einzelglied. Wie viele Glieder muss man aufbiegen?
22. Allgemeines Dreieck (möglichst schiefes Dreieck) für die Schule
Welches ist das schiefste Dreieck? Möglichst schief soll bedeuten, dass der Unterschied der
Innenwinkel des Dreiecks untereinander und zu den Winkeln von 0°, 90° und 180° maximal ist.
23. Zehnstellige Zahl und die Anzahl der verschiedenen Ziffern
Es gibt nur eine zehnstellige Zahl, deren erste Ziffer die Anzahl der Nullen der Zahl
angibt, die zweite Ziffer die Anzahl der Einsen, die dritte Ziffer die Anzahl der Zweien... und die letzte Ziffer
die Anzahl der Neunen. Welche Zahl ist das?
24. Der Pythagorasbaum und seine Blätter
Ein Pythagorasbaum entsteht, wenn man auf ein Quadrat (Stamm) ein
rechtwinkliges Dreieck (Verzweigung) mit seiner Hypotenuse aufsetzt.
An die Katheten schließen sich wieder Quadrate (Zweige) an, an deren
gegenüberliegenden Seiten sich wiederum rechtwinklige Dreiecke befinden, die
dem ersten Dreieck ähnlich sind usw. Alle entstehenden Verzweigungen enden mit
Quadraten (Blättern). Für welche rechtwinkligen Dreiecke ist es möglich, jeden
Pythagorasbaum durch Hinzufügen von weiteren Dreiecken und Quadraten so
wachsen zu lassen, dass er höchstens zwei verschiedene Größen von Blättern besitzt?
25. Regelmäßige Vielecke und Einheitskreis
Einem Einheitskreis werden beliebige regelmäßige Vielecke einbeschrieben und umbeschrieben.
Welche dieser Vielecke haben einen ganzzahligen Flächeninhalt?
26. Hyperwürfel und seine Inkugel und Umkugel
Ein Quadrat hat etwa 63,7% der Fläche seines Umkreises, der zugehörige Inkreis aber etwa 78,5% der Fläche des
Quadrates. Ein Quadrat schmiegt sich also stärker an seinen Inkreis als an seinen Umkreis. Vergleicht man das Volumen eines Würfels mit
dem Volumen seiner Umkugel und dem seiner Inkugel, so findet man diesen Effekt sogar verstärkt. Betrachtet man dagegen Hyperwürfel in
immer höheren Dimensionen, so findet man eine Dimension, in der dieser Effekt maximal wird, dann wieder abnimmt und sich schließlich sogar
umkehrt. Ab welcher Dimension schmiegt sich ein Hyperwürfel stärker an seine Umkugel als an seine Inkugel?

27. Ein Kuchen und die gerechte Aufteilung unter drei Kindern
Gibt es eine Möglichkeit, einen Kuchen so unter drei Kindern aufzuteilen, dass sich kein Kind
aus gutem Grunde beschweren kann, es habe weniger als ein Drittel des Kuchens bekommen?
28. Gespanntes Seil vom Nordpol zum Südpol der Erde
Ein Seil wird straff vom Nordpol zum Südpol der Erde gespannt und anschließend
um 1 Meter verlängert. Wie weit kann man das Seil vom Erdmittelpunkt in Richtung Äquator ziehen, bis es wieder
straff wird, wenn man für den Radius der Erde eine Länge von 6378 km annimmt?

29. Erbschaft und Stammbrüche
Ein reicher Geschäftsmann besaß 41 Firmen. In seinem Testament legte er fest, dass das älteste seiner
drei Kinder die Hälfte seiner Firmen erben sollte, das zweitälteste ein Drittel und das jüngste ein Siebtel. Als der Vater starb,
waren die Kinder ratlos, wie sie den Wunsch des Vaters erfüllen sollten, da sich 41 weder durch 2 noch durch 3 oder durch 7 teilen
ließ. Sie fragten einen gemeinsamen Freund, der eine eigene Firma besaß, ob er ihnen nicht weiterhelfen könnte. Dieser
sagte, dass er den Roman „Per Anhalter durch die Galaxis“ von Douglas Adams gelesen habe. Dort werde berichtet, dass nach den
Berechnungen des Computers "Deep Thought" 42 die Antwort auf die Frage nach dem Leben, dem Universum und dem ganzen Rest sei.
Er machte deshalb den Vorschlag, bei der Aufteilung so zu tun, als wäre seine eigene Firma auch Teil der Erbschaft. Tatsächlich
konnte das nun aus 42 Firmen bestehende Erbe zur vollen Zufriedenheit der Kinder aufgeteilt werden, ohne dass der Freund seine
Firma abgeben musste. Wie war das möglich?
30. Sohn und Tochter
Ein Ehepaar hat zwei Kinder. Es ist bekannt, dass eines der beiden Kinder ein Sohn ist.
Wie groß ist die Wahrscheinlichkeit, dass das Ehepaar auch eine Tochter hat, wenn man annimmt, dass gleich viele
Jungen wie Mädchen geboren werden?
31. Schachbrett, Euromünzen und die Exponentialfunktion
Auf das erste Feld eines Schachbretts wird eine Euromünze mit einer Dicke von 2,33 Millimeter gelegt, auf das zweite Schachfeld
werden zwei Euromünzen gelegt, auf das dritte Schachfeld wieder die doppelte Anzahl usw.. Anschließend wird mit allen Euromünzen
zusammen ein Turm gebaut. Wie hoch ist dieser Turm und womit ist seine Höhe vergleichbar?
32. Der Sultan und seine 6 Söhne
Ein Sultan hatte 6 Söhne. Außerdem besaß er einen Palast mit vielen Kellergewölben.
In jedem Kellergewölbe befanden sich genauso viele Schatztruhen wie im Palast Kellergewölbe vorhanden waren.
Und schließlich enthielt jede Schatztruhe genauso viele Goldmünzen wie Schatztruhen in einem Kellergewölbe standen.
Der Sultan rief nun seinen Schatzkämmerer zu sich und versprach ihm eine Schatztruhe mit Goldmünzen als Belohnung,
wenn es ihm gelänge, den restlichen Schatz so an seine 6 Söhne zu verteilen, dass jeder Sohn genau die gleiche
Anzahl von Goldmünzen bekäme. Ansonsten würde er sein Leben verlieren. Konnte der Schatzkämmerer den Schatz
gleichmäßig verteilen und damit sein Leben retten?
33. Der Wanderer und die drei Himmelsrichtungen
Ein Wanderer läuft erst einen Kilometer nach Süden, dann einen Kilometer nach Osten und schließlich einen Kilometer
nach Norden. Danach befindet er sich wieder am Ausgangspunkt. Wo auf der Erde befindet sich dieser Ausgangspunkt?
34. Platonische Körper im Würfel
Welche platonischen Körper können einem Würfel einbeschrieben werden?
35. Abstände zwischen vier Punkten
Vier Punkte sollen auf einer Ebene an unterschiedlichen Stellen platziert werden. Welche Möglichkeiten gibt es,
die vier Punkte so anzuordnen, dass es unter den sechs Abständen zwischen diesen Punkten nur zwei verschiedene gibt?
36. Regelmäßige Sechsecke im Kreis
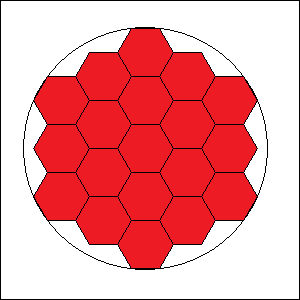
Platziert man in einen Kreis ein einbeschriebenes regelmäßiges Sechseck, so bedeckt es 82,7% der Kreisfläche. Vergrößert
man diesen Kreis, so passen immer mehr parkettartig angeordnete regelmäßige Sechsecke vollständig hinein, wobei sich
das erste Sechseck weiterhin in der Mitte des Kreises befinden soll. Ab welcher Anzahl bedecken diese Sechsecke zum ersten
Mal mehr als 82,7% der Kreisfläche? Die folgende Abbildung zeigt ein Beispiel mit 19 Sechsecken, das aber nicht die Lösung
darstellt.
Stochastik, Lotto, Kniffel und Polyeder
Stochastik-Formeln mit konkreten Beispielen
Wie groß ist die Wahrscheinlichkeit für 6 Richtige beim Lotto 6 aus 49?
Kniffel - Wahrscheinlichkeiten und Punktzahlen bei optimaler Strategie
Wie groß ist die Wahrscheinlichkeit für einen Kniffel mit drei Würfen von jeweils fünf
Würfeln bei optimaler Strategie?
Weitere Wahrscheinlichkeiten und optimale Strategien beim Kniffel
Was sind die optimalen Strategien in der ersten Runde beim Kniffel?
Wahrscheinlichkeiten beim Poker
Wie groß ist die Wahrscheinlichkeit, beim Texas Hold’em auf Anhieb einen Flush zu erzielen?
Lotto 6 aus 49 und die Strategie für überdurchschnittliche Lottoquoten
Mit welchen Zahlen erzielt man im Mittel überdurchschnittliche Quoten bei Lotto 6 aus 49? Welches sind die unbeliebtesten Zahlen?
EuroJackpot - Gewinnchancen und Gewinnquoten
Wie groß ist die Wahrscheinlichkeit für 5 richtige Zahlen und 2 richtige Eurozahlen bei EuroJackpot?
EuroJackpot und die Strategie für überdurchschnittliche Quoten
Mit welchen Zahlen erzielt man im Mittel überdurchschnittliche Quoten bei EuroJackpot?
Platonische Körper und Archimedische Körper
Welcher platonische oder archimedische Körper hat die größte Kugelähnlichkeit?
Platonische und Archimedische Parkettierungen
Wie viele archimedische Parkettierungen gibt es?
Geodätische Kuppeln
Was sind geodätische Kuppeln und wie erzeugt man sie?
Leben, Erde und Universum
Großkreisentfernung zwischen zwei Orten
Wie weit ist es von Hamburg bis Tokio?
Reisezeiten mit einer globalen Magnetschwebebahn
Wie lange dauert theoretisch eine Reise mit einer globalen Magnetschwebebahn um die halbe Erde?
Zeitdilatation (Zeitdehnung) auf der Erdoberfläche, im Flugzeug und auf der ISS
In welcher Entfernung müsste ein Raumschiff um die Erde kreisen, damit dort die Zeit genauso schnell vergeht wie auf der Erde?
Das Leben auf der Erde und seine Masse
Was wiegen alle Lebewesen auf der Erde zusammengenommen?
"Weltuntergänge"
Wann und wodurch könnte die Welt "untergehen"?
Die Geburt und die 13 Sternbilder
Wer wurde im Sternbild Schlangenträger geboren?
Größenvergleich (Objekte im Mikrokosmos, im Alltag und im Universum)
Wie kann man sich Größen und Entfernungen in unserem Sonnensystem anschaulich vorstellen?
Reisezeiten mit einem interstellaren Raumschiff
Wie lange dauert theoretisch eine Reise mit einem interstellaren Raumschiff zum Polarstern?
Möglichkeiten und Grenzen bemannter Raumfahrt
Werden Menschen jemals Planeten fremder Sternensysteme erreichen?
Außerirdisches Leben in unserer Milchstraße (eine vorsichtige Abschätzung)
Wie viele intelligente Zivilisationen leben gegenwärtig in unserer Galaxis?
Impressum und interessante Links
Copyright © Werner Brefeld (2005)







